Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm câu cuối nhá bài này dễ ợt ý mà
Gọi góc BAC = ♪ ( cho sinh độg) =))
Thì góc BHC = 180 – ♪
Vì D là trung điểm MH => ∆ CMH cân
=> ∆ CMB = ∆ CHB (c.c.c)
=> Góc CMB bằng góc CHB = 180 – ♪
Mà A,H,D thẳng hàng và H Đối xứng với M qua trục BC
Đến đây đủ để kết luận là
Đường tròn ở sẽ đối xứng với đường tròn ngoại tiếp ∆ BHC
Nên (O) =(I)
= 2πR
Với I là tâm

a) Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) cùng nhìn cạnh BC một góc bằng 900
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

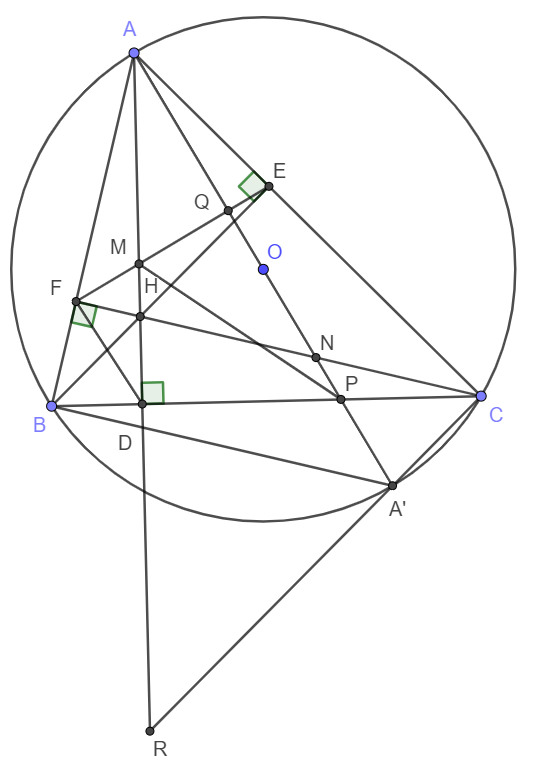
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm
O A B C M H F E D
a)
Vì \(\widehat{HFB}+\widehat{HDB}=180^o\)=> Tứ giác BFHD nội tiếp
Vì \(\widehat{BFC}=\widehat{BEC}=90^o\)=> Tứ giác BFEC nội tiếp
b) Xét tam giác BDH và tam giác BEC có: \(\widehat{BDH}=\widehat{BEC}=90^o\), \(\widehat{B_1}\)chung
=> Tam giác BDH đồng dạng tam giác BEC
=> \(\frac{BD}{BH}=\frac{BE}{BC}\)=> BD.BC=BE.BH
c) \(\widehat{BCM}=\widehat{BAM}\)( cùng chắn cung BM của đường tròn (O)) (1)
vì \(\widehat{ADC}=\widehat{CFA}=90^o\)=> Tứ giác AFDC nội tiếp
=> \(\widehat{FAD}=\widehat{FCD}\) hay \(\widehat{BAM}=\widehat{HCB}\) (2)
Từ (1) , (2)
=> \(\widehat{BCM}=\widehat{BCH}\)=> CD là đường phân giác của tam giác HCM mà CD cũng là đường cao
=> HCM cân tại C=> D là trung điểm HM
c) Câu hỏi của Nguyễn Vy - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo link này nhé!