Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

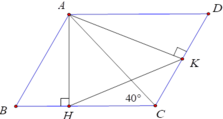
Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B

Bài 12:
:v Mình sửa P là trung điểm của EG
A B C D E O Q N F G M I 1 2 P
a) Ta có: \(\widehat{EAC}=\widehat{EAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{GAB}=\widehat{GAC}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\Rightarrow\widehat{EAC}=\widehat{GAB}\)
Xét tam giác EAC và tam giác BAG có:
\(\hept{\begin{cases}EA=AB\\\widehat{EAC}=\widehat{GAB}\left(cmt\right)\\AG=AC\end{cases}}\Rightarrow\Delta EAC=\Delta BAG\left(c-g-c\right)\)
\(\Rightarrow CE=BG\)( 2 cạnh t. ứng )
+) Gọi O là giao điểm của EC và BG, Gọi I là giao điểm của AC và BG
Vì \(\Delta EAC=\Delta BAG\left(cmt\right)\)
\(\Rightarrow\widehat{ACE}=\widehat{AGB}\)
Vì tam giác AIG vuông tại A nên \(\widehat{I1}+\widehat{AGB}=90^0\)(2 góc phụ nhau )
Mà \(\widehat{ACE}=\widehat{AGB}\left(cmt\right),\widehat{I1}=\widehat{I2}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{I2}+\widehat{ACE}=90^0\)
Xét tam giác OIC có \(\widehat{I2}+\widehat{ACE}+\widehat{IOC}=180^0\left(dl\right)\)
\(\Rightarrow\widehat{IOC}=90^0\)
\(\Rightarrow BG\perp EC\)
b) Vì ABDE là hình vuông (gt)
\(\Rightarrow EB\)cắt AD tại Q là trung điểm của mỗi đường (tc)
Xét tam giác EBC có Q là trung điểm của EB (cmt) , M là trung điểm của BC (gt)
\(\Rightarrow QM\)là đường trung bình của tam giác EBC
\(\Rightarrow QM=\frac{1}{2}EC\left(tc\right)\)
CMTT: \(PN=\frac{1}{2}EC;QP=\frac{1}{2}BG,MN=\frac{1}{2}BG\)
Mà EC=BG (cm câu a )
\(\Rightarrow QM=MN=NP=PQ\)
Xét tứ giác MNPQ có \(QM=MN=NP=PQ\left(cmt\right)\)
\(\Rightarrow MNPQ\)là hình thoi ( dhnb ) (1)
CM: MN//BG , QM//EC ( dựa vào đường trung bình tam giác )
Mà \(BG\perp EC\left(cmt\right)\)
\(\Rightarrow MN\perp MQ\)
\(\Rightarrow\widehat{QMN}=90^0\)(2)
Từ (1) và (2) \(\Rightarrow MNPQ\) là hình vuông ( dhnb )
\(\)
Bài 11:
A B C H D P E Q
a) Ta có: \(\widehat{HAD}+\widehat{HAE}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{DAE}=180^0\)
\(\Rightarrow D,A,E\)thẳng hàng
b) Vì AHBD là hình chữ nhật (gt)
\(\Rightarrow AB\)cắt DH tại trung điểm mỗi đường (tc) và AB=DH(tc)
Mà P là trung điểm của AB (gt)
\(\Rightarrow P\)là trung điểm của DH (1)
\(\Rightarrow PH=\frac{1}{2}DH,PA=\frac{1}{2}AB\)kết hợp với AB=DH (cmt)
\(\Rightarrow PH=PA\)
\(\Rightarrow P\in\)đường trung trục của AH
CMTT Q thuộc đường trung trực của AH
\(\Rightarrow PQ\)là đường trung trực của AH
c) Từ (1) => P thuộc DH
=> D,P,H thẳng hàng
d) Vì ABCD là hình chữ nhật (gt)
=> DH là đường phân giác của góc BHA (tc) mà góc BHA= 90 độ
=> góc DHA= 45 độ
CMTT AHE =45 độ
=> góc DHA+ góc AHE=90 độ
Hay góc DHE=90 độ
=> DH vuông góc với HE

Xét tam giác AHB và tam giác AKC
^A _ chung ; AB = AC
Vậy tam giác AHB = tam giác AKC (ch-gn)
=> AH/AK = AB/AC => AH/AB = AK/AC
Xét tam giác AKH và tam giác ACB có
^A _ chung; AH/AB = AK/AC
Vậy tam giác AKH ~ tam giác ACB (c.g.c)

░░█▒▒▒▒░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒█ ░░░░█▒▒▄▀▀▀▀▀▄▄▒▒▒▒▒▒▒▒▒▄▄▀▀▀▀▀▀▄ ░░▄▀▒▒▒▄█████▄▒█▒▒▒▒▒▒▒█▒▄█████▄▒█ ░█▒▒▒▒▐██▄████▌▒█▒▒▒▒▒█▒▐██▄████▌▒█ ▀▒▒▒▒▒▒▀█████▀▒▒█▒░▄▒▄█▒▒▀█████▀▒▒▒█ ▒▒▐▒▒▒░░░░▒▒▒▒▒█▒░▒▒▀▒▒█▒▒▒▒▒▒▒▒▒▒▒▒█ ▒▌▒▒▒░░░▒▒▒▒▒▄▀▒░▒▄█▄█▄▒▀▄▒▒▒▒▒▒▒▒▒▒▒▌ ▒▌▒▒▒▒░▒▒▒▒▒▒▀▄▒▒█▌▌▌▌▌█▄▀▒▒▒▒▒▒▒▒▒▒▒▐ ▒▐▒▒▒▒▒▒▒▒▒▒▒▒▒▌▒▒▀███▀▒▌▒▒▒▒▒▒▒▒▒▒▒▒▌ ▀▀▄▒▒▒▒▒▒▒▒▒▒▒▌▒▒▒▒▒▒▒▒▒▐▒▒▒▒▒▒▒▒▒▒▒█ ▀▄▒▀▄▒▒▒▒▒▒▒▒▐▒▒▒▒▒▒▒▒▒▄▄▄▄▒▒▒▒▒▒▄▄▀ ▒▒▀▄▒▀▄▀▀▀▄▀▀▀▀▄▄▄▄▄▄▄▀░░░░▀▀▀▀▀▀ ▒▒▒▒▀▄▐▒▒▒▒▒▒▒▒▒▒▒▒▒▐ ▒█▀▀▄ █▀▀█ █▀▀█ █▀▀█ ▀▀█▀▀ █░░█ █▀▀ ▒█▀▀█ █▀▀█ █▀▀ █▀▀ ▒█░▒█ █▄▄▀ █░░█ █░░█ ░▒█░░ █▀▀█ █▀▀ ▒█▀▀▄ █▄▄█ ▀▀█ ▀▀█ ▒█▄▄▀ ▀░▀▀ ▀▀▀▀ █▀▀▀ ░▒█░░ ▀░░▀ ▀▀▀ ▒█▄▄█ ▀░░▀ ▀▀▀ ▀▀▀ ║████║░░║████║████╠═══╦═════╗ ╚╗██╔╝░░╚╗██╔╩╗██╠╝███║█████║ ░║██║░░░░║██║╔╝██║███╔╣██══╦╝ ░║██║╔══╗║██║║██████═╣║████║ ╔╝██╚╝██╠╝██╚╬═██║███╚╣██══╩╗ ║███████║████║████║███║█████║
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)