Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC


a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

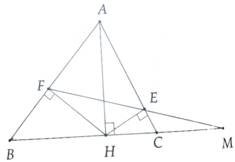
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)

c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AFE
=>Ax//EF
=>EF vuông góc OA

b) Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\left(=\widehat{AEF}\right)\)
\(\widehat{M}\) chung
Do đó: ΔMEB\(\sim\)ΔMCF(g-g)
Suy ra: \(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
hay \(ME\cdot MF=MB\cdot MC\)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)(hai góc tương ứng)

ĐỀ BÀI THIẾU \(\widehat{BAC}=105^0\). Hình vẽ trong TKHĐ

Qua A kẻ đường thẳng vuông góc với AC cắt BC tại M. Tại E kẻ đường thẳng song song với AH cắt AC tại D.
Xét tam giác ABE có AB=BE=1 mà ^ABE=600 nên tam giác ABE đều. Khi đó
\(AH=AB\cdot\sin\widehat{ABH}=\sin60^0=\frac{\sqrt{3}}{2}\)
Dễ thấy \(\Delta MAE=\Delta ADE\left(g.c.g\right)\Rightarrow AD=AM\Rightarrow\Delta\)AMC vuông tại A có đường cao AH theo hệ thức lượng:
\(\frac{1}{AC^2}+\frac{1}{AM^2}=\frac{1}{AH^2}\Rightarrow\frac{1}{AC^2}+\frac{1}{AD^2}=\frac{1}{\left(\frac{\sqrt{3}}{2}\right)^2}=\frac{4}{3}\)

Gọi F đối xứng với C qua A. Khi đó tam giác FBC vuông tại F.
Theo hệ thức lượng thì \(BC^2=HC\cdot CF\). Mặt khác \(BC^2=2AB\cdot HC\)
Đến đây dễ rồi nha, làm tiếp thì chán quá :(