Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔMNP vuông tại M, ta được:
\(NP^2=MN^2+MP^2\)
\(\Leftrightarrow NP^2=36^2+48^2=3600\)
hay NP=60(cm)
Xét ΔMNP có MK là đường phân giác ứng với cạnh NP(gt)
nên \(\dfrac{NK}{MN}=\dfrac{KP}{MP}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{NK}{36}=\dfrac{KP}{48}\)
mà NK+KP=NP=60cm(K nằm giữa N và P)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{NK}{36}=\dfrac{KP}{48}=\dfrac{NK+KP}{36+48}=\dfrac{60}{84}=\dfrac{5}{7}\)
Do đó:
\(\dfrac{NK}{36}=\dfrac{5}{7}\)
hay \(NK=\dfrac{180}{7}cm\)
Vậy: \(NK=\dfrac{180}{7}cm\)

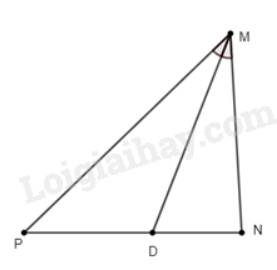
Vì \(MD\) là tia phân giác góc \(M\left( {D \in NP} \right)\) nên theo tính chất đường phân giác ta có:
\(\frac{{DN}}{{DP}} = \frac{{MN}}{{MP}};\frac{{DN}}{{MN}} = \frac{{DP}}{{MP}};\frac{{DP}}{{DN}} = \frac{{MP}}{{MN}};\frac{{DP}}{{MP}} = \frac{{DN}}{{MN}}\)
a) Xét ΔMNP có MD là đường phân giác ứng với cạnh NP(gt)
nên \(\frac{ND}{NM}=\frac{DP}{PM}\)
\(\Leftrightarrow\frac{ND}{8}=\frac{7.5}{10}\)
hay \(ND=\frac{7.5\cdot8}{10}=\frac{60}{10}=6cm\)
Vậy: ND=6cm
b) Xét ΔMNP có DC//MP(gt)
nên \(\frac{NC}{CM}=\frac{ND}{DP}\)
\(\Leftrightarrow\frac{NC}{CM}=\frac{6}{7.5}\)
hay \(\frac{NC}{6}=\frac{CM}{7.5}\)
Ta có: NC+CM=MN=8cm(C nằm giữa N và M)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{NC}{6}=\frac{CM}{7.5}=\frac{NC+CM}{6+7.5}=\frac{NM}{13.5}=\frac{8}{13.5}=\frac{16}{27}\)
Do đó: \(\frac{NC}{6}=\frac{16}{27}\)
\(\Leftrightarrow NC=\frac{16\cdot6}{27}=\frac{96}{27}=\frac{32}{9}\simeq3.55cm\)
Vậy: NC\(\simeq\)3,55cm