Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

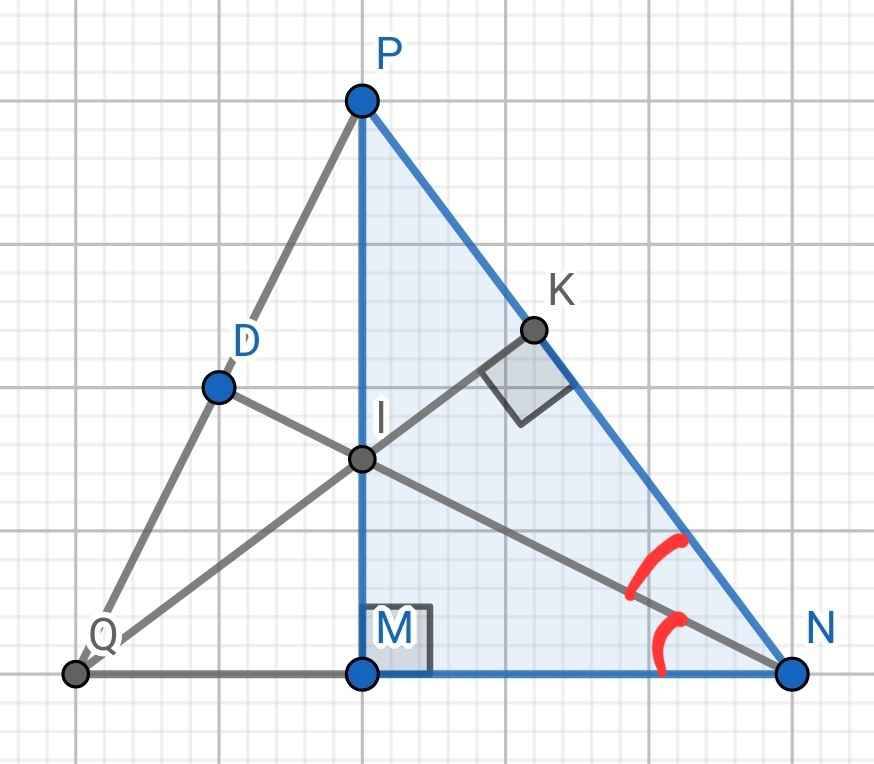
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

a) tam giác MNP có MN=MP(GT) suy ra tam giác MNP cân tại M (ĐỊNH nghĩa tam giác cân)
b) xét tam giác MNI và MPI có
MI chung
MN=MP(GT)
IN=IP(MI là trung tuyến nên I là trung điểm NP)
SUY ra tam giác MNI=MPI(C-C-C)
c) Vì tam giác MNP cân tại M(cmt)màMI là đường trung tuyến nên MI đồng thời cũng là đường cao đường trung trực hay MI là đường trung trực của NP (tính chất tam giác cân)
d)Vì MI là đường cao tam giác MNP(cmt) suy ra MI vuông góc với NP suy ra tam giác MNI vuông tại I
Vì MI là đường trung tuyến nên I là trung điểm NP suy ra NI=1/2NP
Mà NP=12cm(gt) suy ra NI=12x1/2=6cm
xét tam giác vuông MNI có
NM2=NI2+MI2(ĐỊNH LÍ Py-ta-go)
Suy ra MI2=NM2-NI2
mà NM=10CM(gt) NI=6CM(cmt)
suy ra MI2=102-62=100-36=64=căn bậc 2 của 64=8
mà MI>0 Suy ra MI=8CM (đpcm)
ế) mik gửi cho bn bằng này nhé
a) Vì MN=MP => tam giác MNP là tam giác cân tại M.
b)Xét tam giác MIN và tam giác MIP có:
MN=MP (vì tam giác MNP cân)
\(\widehat{MNP}=\widehat{MPI}\)(tam giác MNP cân)
NI=PI(vì MI là trung tuyến)
=> tam giác MIN=tam giác MIP(c.g.c)
c) Ta có: MN=MP
IN=IP
=> M,I thuộc trung trực của NP
Hay MI là đường trung trực của NP
d) IN=IP=NP/2=12/2=6(cm)
Xét tam giác MIN có góc MIN =90*
=> MN^2=MI^2 + NI^2
=> MI^2=MN^2-NI^2
=> MN^2 = 10^2 - 6^2
=> MN = 8
e) Tam giác HEI có goc IHE=90*
=> góc HEI + góc HIE= 90*
Mà góc HIE = góc MEF/2
=> góc MEF/2 + góc HEI = 90* (1)
Mà góc MEF + góc HEI + góc IEF = 180*
=> góc MEF/2 + góc IEF = 90* (2)
Từ (1) và (2) => góc HEI = góc IEF
Hay EI là tia phân giác của góc HEF

a: ta có: ΔMNP cân tại M
mà MH là đường cao
nên H là trung điểm của NP
hay HN=HP
b: NH=NP/2=8/2=4(cm)
=>MH=3(cm)
c: Xét ΔMDH vuông tại D và ΔMEH vuông tại E có
MH chung
\(\widehat{DMH}=\widehat{EMH}\)
Do đó: ΔMDH=ΔMEH
Suy ra: HD=HE
hay ΔHED cân tại H
Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK