Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

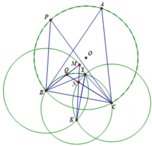
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.

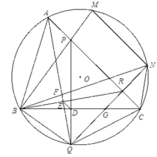
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q

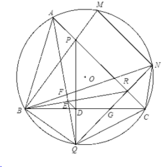
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

A B C O I M N P Q L K J
Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).

Gọi cạnh tam giác là a thì \(a=R\sqrt{3}\)
Do tính đối xứng của đường tròn và tam giác đều, không mất tính tổng quát, giả sử M nằm trên cung nhỏ BC
\(\Rightarrow\widehat{BMC}=180^0-\widehat{BAC}=120^0\)
\(\Rightarrow AM.BC=AB.CM+AC.BM\Leftrightarrow AM=BM+CM\)
\(\Rightarrow S=\left(BM+CM\right)^2+2BM^2-3CM^2\)
\(=3BM^2+2BM.CM-2CM^2\)
Lại có: \(BC^2=BM^2+CM^2-2MB.MC.cos\widehat{BMC}\)
\(=BM^2+CM^2+MB.MC\Rightarrow MB.MC=3R^2-BM^2-CM^2\)
\(\Rightarrow S=6R^2+BM^2-4CM^2\)
Gọi I là điểm thỏa mãn \(\overrightarrow{BI}-4\overrightarrow{CI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BC}\)
\(\Rightarrow BI=\dfrac{4\sqrt{3}}{3}R\) ; \(CI=\dfrac{\sqrt{3}}{3}R\)
\(S=6R^2+\left(\overrightarrow{BI}+\overrightarrow{IM}\right)^2-4\left(\overrightarrow{CI}+\overrightarrow{IM}\right)^2\)
\(S=6R^2+BI^2-4CI^2-3IM^2=10R^2-3IM^2\)
\(S_{max}\) khi \(IM_{min}\Rightarrow M\equiv C\Rightarrow S=CA^2+2CB^2=9R^2\)

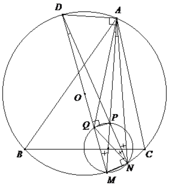
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.
Bạn ơi ở đây ko có một hình ảnh hay text nào hết ????
Giải hộ mình với