Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ tớ có lẽ vẽ hơi chi tiết về phần bằng nhau hay vuông góc nhỉ ???? Nếu không nhìn thấy rõ thì bảo tớ vẽ lại nhé ;)

a)
Theo đề ra, ta có: ED= 6 (cm) => \(ED^2=6^2=36\)
DF=8(cm) => \(DF^2=8^2=64\)
EF=10(cm) => \(EF^2=10^2=100\)
Ta thấy: 100= 36+64 => \(EF^2=DE^2+DF^2\)
=> Tam giác EDF vuông tại D (theo định lý Py-ta-go đảo)
b)
*) Xét \(\Delta EDM\) và \(\Delta ENM\), có:
ED=EN(gt)
\(\widehat{E_1}=\widehat{E_2}\)
Chung EM.
=> \(\Delta EDM=\Delta ENM\left(c.g.c\right)\) ( còn có cách g.c.g nữa )
=> \(\widehat{EDM}=\widehat{ENM}\) và DM=MN mà \(\widehat{EDM}=90^o\)
=> \(\widehat{ENM}=90^o\) => MN vuông góc với EF.
*) Trong tam giác NMF vuông tại N => Góc N là góc lớn nhất trong tam giác đó => MF là cạnh lớn nhất => MF>MN.
Mà MN=DM => MF>DM.
c) Lấy điểm giao nhau của EM và DN là P'
Xét tam giác EDP' và tam giác ENP', ta có:
ED=EN
\(\widehat{E_1}=\widehat{E_2}\)
Chung EP'
=> \(\Delta EDP'=\Delta ENP'\left(c.g.c\right)\)
=> DP'=P'N => P' là trung điểm của đoạn thẳng DN mà P cũng là trung điểm của đoạn thẳng DN nên P và P' trùng nhau.
Đồng thời P và M cùng nằm trên tia phân giác của góc E.(1)
*) Nối điểm E-> Q ( phải nối vì ta chưa chứng minh được Q thuộc tia phân giác góc E ý mà)
Xét tam giác DMI và tam giác NMF.
\(\widehat{D}=\widehat{N}\left(=90^o\right)\)
DM=MN
\(\widehat{M_1}=\widehat{M_2}\) (góc đối đỉnh)
=> \(\Delta DMI=\Delta NMF\left(g.c.g\right)\)
=> DI=NF và ED=EN => DI+DE=FN+FE =>IE=FE
Xét tam giác EQI và tam giác EQF.
IE=FE
Chung EQ
IQ=QF( do Q là trung điểm của IF)
=> \(\Delta EIQ=\Delta EFQ\left(c.c.c\right)\) => \(\widehat{E_1}=\widehat{E_2}\) => Q thuộc tia phân giác của góc E (2)
Từ (1) và (2) => P,M,Q thẳng hàng......
p/s: Nếu cậu thích thì có thể không làm theo dạng xét tam giác mà áp dụng tính chất tia phân giác của góc hay đại loại là thế mà làm .....
Sr về cái hình nha ..... cái hình đánh dấu cái không đáng :p

a: ED<EF
=>HD<HF
b: Xét ΔDEI có DE=DI và góc D=60 độ
nên ΔDEI đều
c: Xét tứ giác FEBD có
A là trung điểm chung của FB và ED
=>FEBD là hbh
=>FE//BD
=>BD vuông góc DE

Ý C là ghi sai đề bài rồi nhé
Còn ý d khó nhất thì giải như sau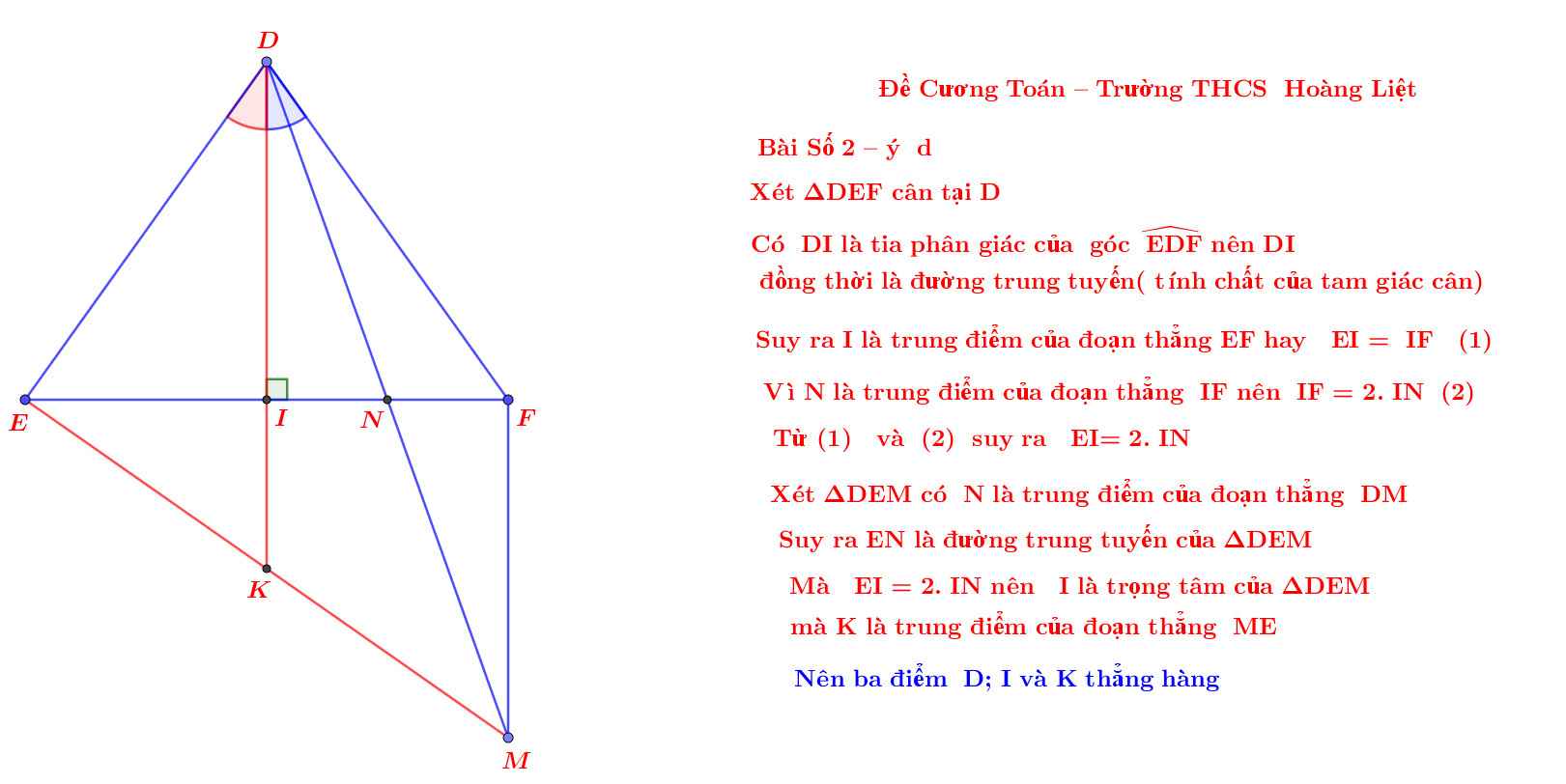

a) Gọi K là giao điểm của EI và DM
Xét \(\Delta EKD\)và \(\Delta EKM\)có :
\(\widehat{E}_1=\widehat{E}_2\)( vì EI là tia phân giác )
\(EI\): Cạnh chung
\(\widehat{EKD}=\widehat{EKM}=90^o\)( GT)
Do đó : Tam giác vuông EKM = Tam giác vuông EKM
\(\Rightarrow ED=EM\)( cặp cạnh tương ứng )
b)
Xét \(\Delta EDI\)và \(\Delta EMI\)có :
\(ED=EM\)( câu a )
\(\widehat{E}_1=\widehat{E_2}\)( vì phân giác )
\(EI:\)Cạnh chung
Do đó : Tam giác EMI = tam giác EDI (c.g.c )
\(\Rightarrow\widehat{EDI}=\widehat{EMI}\)( cặp góc tương ứng )
Mà \(\widehat{EDI}=90^o\)
\(\Rightarrow\widehat{EMI}=90^o\)
\(\Rightarrow\Delta EMI\)là tam giác vuông ( đpcm)
c)
Vì \(\widehat{EMI}=90^o\)( câu b )
\(\Rightarrow\widehat{IMF}=90^o\)
Xét tam giác IMF ta có :
\(\widehat{IMF}=90\)
=> IF là cạnh lớn nhất ( cạnh đối diện với góc vuông )
\(\Rightarrow IF>IM\)
Mà \(IM=ID\)( Vì tam giác EDI = tam giác EMI )
\(\Rightarrow IF>ID\)
c ) Áp dụng t/c đường đồng quy .
\(a,\left\{{}\begin{matrix}DE=DF\\\widehat{EDI}=\widehat{FDI}\\DI\text{ chung}\end{matrix}\right.\Rightarrow\Delta DEI=\Delta DFI\left(c.g.c\right)\\ \Rightarrow\widehat{DIE}=\widehat{DIF};EI=FI\\ \text{Mà }\widehat{DIE}+\widehat{DIF}=180^0\\ \Rightarrow\widehat{DIE}=\widehat{DIF}=90^0\\ \Rightarrow DI\perp EF\text{ và }I\text{ là trung điểm }EF\\ b,\left\{{}\begin{matrix}DE=DF\\\widehat{EDM}=\widehat{FDM}\\DM\text{ chung}\end{matrix}\right.\Rightarrow\Delta DEM=\Delta DFM\left(c.g.c\right)\\ \Rightarrow ME=MF;\widehat{DEM}=\widehat{DFM}=90^0\\ \Rightarrow\Delta AFM\text{ vuông tại }F\)