Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔDEM và ΔDFM có
DE=DF
EM=FM
DM chung
Do đó: ΔDEM=ΔDFM
b: Ta có: ΔDEF cân tại D
mà DM là đường trung tuyến
nên DM là đường cao
c: Xét tứ giác DENF có
M là trung điểm của DN
M là trung điểm của FE
Do đó: DENF là hình bình hành
Suy ra: DE//FN

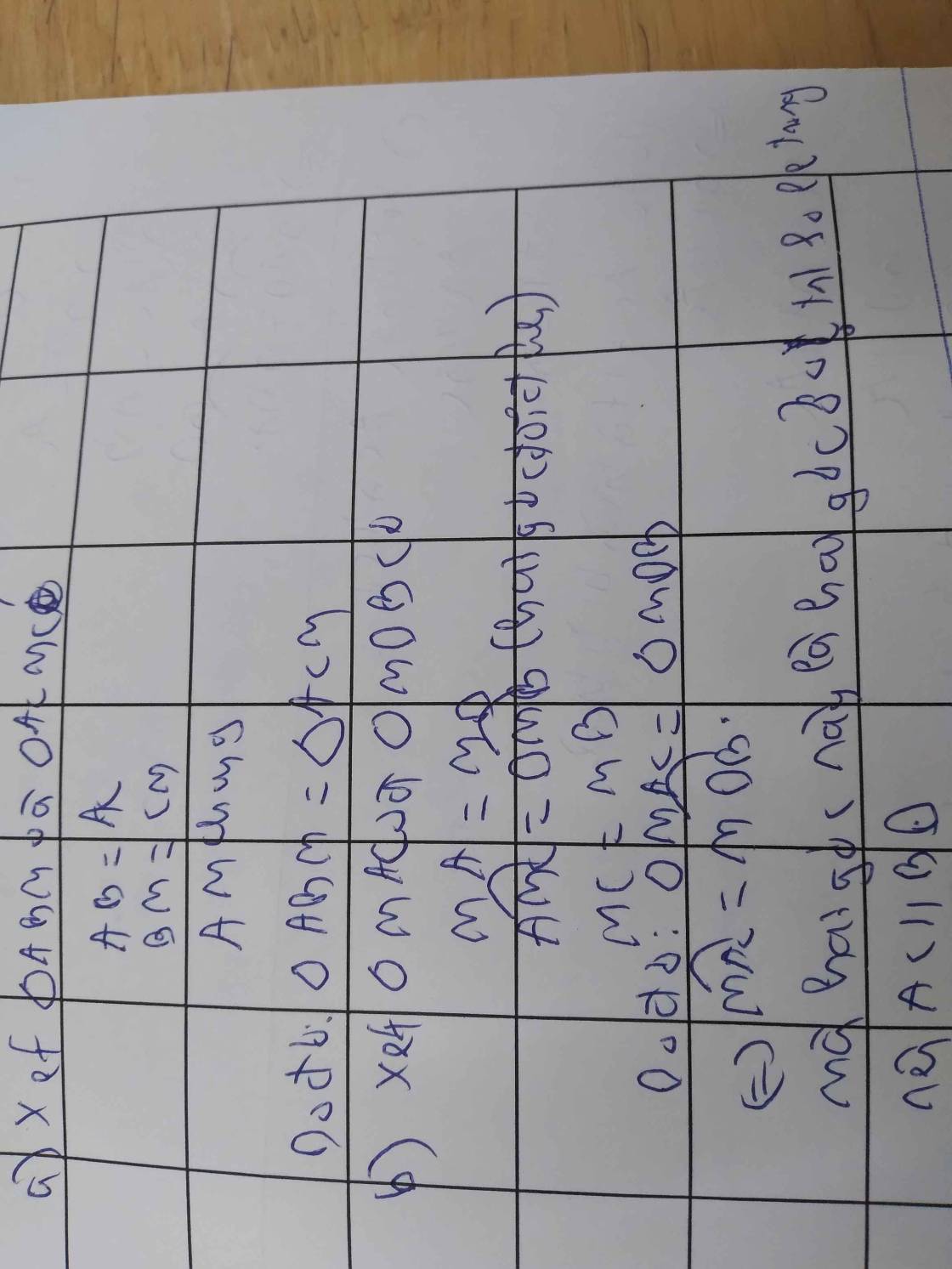
a) Xét △DEM và △KFM có
DM=KM(giả thiết)
góc DME=góc KMF(2 góc đối đỉnh)
EM=MF(Vì M là trung điểm của EF)
=>△DEM =△KFM(c-g-c)
=> góc MDE=góc MKF (2 góc tương ứng)
hay góc EDK= góc EKD mà 2 góc này là 2 góc so le trong bằng nhau của đường thẳng DK cắt 2 đường thẳng DE và KF
=>DE//KF
b) ta có DH⊥EF hay DP⊥EF => góc DHE =góc PHE =90 độ
Xét △DHE (góc DHE=90 độ)△PHE(góc PHE=90 độ) có
HD=HP
HE là cạnh chung
=> △DHE= △PHE(2 cạnh góc vuông)
=> góc DEM=góc PEM
=> EH là tia phân giác của góc DEP
hay EF là tia phân giác của góc DEP
vậy EF là tia phân giác của góc DEP

a, tu ve hinh :
tamgiac ABC can tai A => AB = AC va goc ABC = goc ACB (gn)
goc AIC = goc AIB = 90 do AI | BC (gt)
=> tamgiac AIC = tamgiac AIB (ch - gn)
=> IB = IC (dn)
b, dung PY-TA-GO
c, AE = AF (gt) => tamgiac AFE can tai E (dn)
=> goc AFE = (180 - goc BAC) : 2 (tc)
tamgiac ABC can tai A (gt) => goc ACB = (180 - goc BAC) : 2 (tc)
=> goc AFE = goc ACB ma 2 goc nay dong vi
=> EF // BC (dh)
vay_

a, Xét 2 tam giác vuông DEM và HEM có:
ME cạnh chung
\(\widehat{DEM}\)=\(\widehat{HEM}\)(gt)
=> tam giác DEM=tam giác HEM(CH-GN)
b, vì tam giác DEM=tam giác HEM(câu a) suy ra MD=MH(2 cạnh tương ứng)
c, trong tam giác FKE có: FD,KH là 2 đường cao cắt nhau tại M
=> K,M,H thẳng hàng
D E F M H K

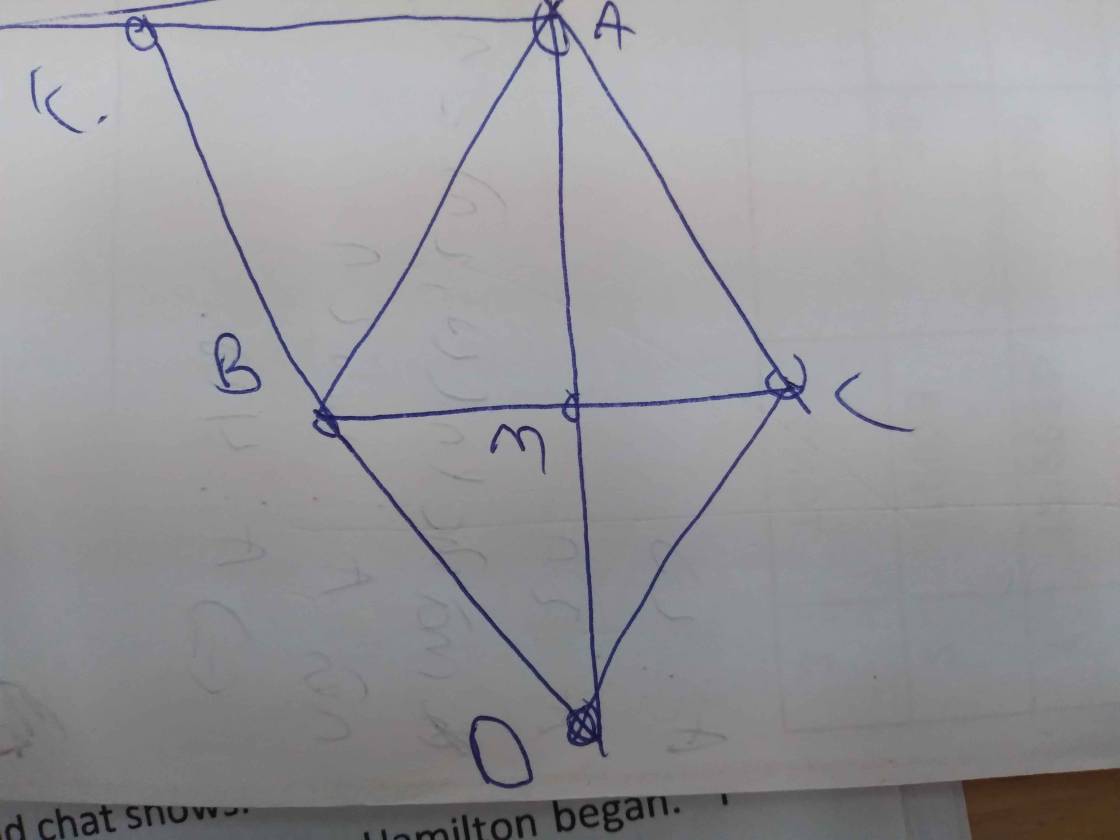
a. Xét tam giác BMC và tam giác DMA có
MB=MD(gt) BMC=DMA(đối đỉnh)
MA=MC(vì M là trung điềm AC)
Vậy tam giác BMC = tam giác DMA(c-g-c)
=>MBC=MDA( 2 góc tương ứng)
=> AD // BC
b. Xét tam giác AMB và tam giác CMD có
MA=MC(vì M là trung điềm AC)
AMB=CMD( đối đỉnh)
MB=MD(gt)
Vậy tam giác AMB = tam giác CMD(c-g-c)
=> AB=CD(2 cạnh tương ứng)
mà AB=AC(vì tam giác ABC cân tại A)
=> AC=CD
=> tam giác ACD cân tại C
c. trong tam giác DEB có M là trung điểm của BD( vì MD=MB)
=> EM là đường trung tuyến thứ nhất (1)
mặt khác AC=CE(gt)
MC=1/2 AC (vì M là trung điềm AC)
=> MC= 1/2 CE

a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

a) Do ∆DEF cân tại D (gt)
⇒ DE = DF
Do M là trung điểm của EF (gt)
⇒ ME = MF
Xét ∆DEM và ∆DFM có:
DE = DF (cmt)
DM là cạnh chung)
ME = MF (cmt)
⇒ ∆DEM = ∆DFM (c-c-c)
b) Sửa đề: Chứng minh DM ⊥ EF
Do ∆DEM = ∆DFM (cmt)
⇒ ∠DME = ∠DMF (hai góc tương ứng)
Mà ∠DME + ∠DMF = 180⁰ (kề bù)
⇒ ∠DME = ∠DMF = 180⁰ : 2 = 90⁰
⇒ DM ⊥ EF
c) Xét ∆DEM và ∆KFM có:
DM = KM (gt)
∠DME = ∠KMF (đối đỉnh)
ME = MF (cmt)
⇒ ∆DEM = ∆KFM (c-g-c)
⇒ DE = KF (hai cạnh tương ứng)
Mà DE = DF (cmt)
⇒ KF = DF
⇒ ∆FDK cân tại F