Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{ABH};\widehat{ACK}\) là các góc phụ với A
b: Vì \(\widehat{ABH}+\widehat{A}=90^0\)
mà \(\widehat{ACK}+\widehat{A}=90^0\)
nên \(\widehat{ABH}=\widehat{ACK}\)
\(\widehat{BIK}=\widehat{CIH}\)(hai góc đối đỉnh)

Bài 3:
\(\widehat{xAC}=\dfrac{180^0-80^0}{2}=50^0\)
\(\Leftrightarrow\widehat{xAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//BC
Bài 15:
\(\widehat{ABH}+\widehat{A}=90^0\)
\(\widehat{ACK}+\widehat{A}=90^0\)
Do đó: \(\widehat{ABH}=\widehat{ACK}\)

Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)
Tam giác ABH vuông tại H
\(\Rightarrow\)\(ABH+A=90^o\) (tính chất tam giác vuông)
\(\Rightarrow\)\(ABH=90-A\)\(\left(1\right)\)
Tam giác ACK vuông tại K
\(\Rightarrow\)\(ACK+A=90^0\)(tính chất tam giác vuông)
\(ACK=90^o-A\)\(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\)\(ABH=ACK\)

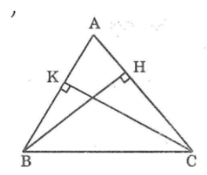
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)

a) Xét 2 tam giác vuông: tam giác ABH và tam giác ACK có:
AB = AC (gt)
góc A chung
suy ra: tam giác ABH = tam giác ACK (ch-gn)
b) áp dụng định lí tổng 3 góc của tam giác vào tam giác vuông ABH ta có:
góc BAH + góc ABH = 90^0
=> góc ABH = 90^0 - góc BAH
=> góc ABH = 90^0 - 50^0 = 40^0
Tam giác ABC cân tại A => \(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}=65^0\)
=> góc HBC = 25^0
Tương tự: góc KCB = 25^0
suy ra: góc BOC = 130^0

BTS là cục cứt chó j , nó đéo xứng làm cục cứt của the coconut tao
con kia là đồ giả mạo
Mà ông Duy có j hay đâu mà bọn m giả lắm thế