Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A D E B C M N
a, xét tam giác ABD và tam giác ACE có : BD = CE (Gt)
góc ADB = góc AEC do tam giác ADE cân tại A (gt)
AD = AE do tam giác ADE cân tại A (gt)
=> tam giác ABD = tam giác ACE (c-g-c)
=> AB = AC (đn)
=> tam giác ABC cân tại A (đn)
b, tam giác ADE cân tại A (gt)
=> góc ADE = (180 - góc D) : 2
góc D = 65 (gt)
=> góc ADE = (180 - 65) : 2 = ...
c, xét tam giác DMB và tam giác ENC có : BD = CE (gt)
góc ADE = góc AED (câu a)
góc DMB = góc ENC = 90
=> Tam giác DMB = tam giác ENC (ch-gn)
d, dùng pytago tính ra AM = 8
cm AM = AN
=> AN = 8

A D E I B C M N
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
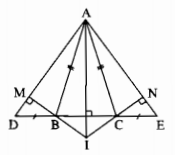
a) Xét ∆ADE cân tại A nên góc D = góc E
Xét ∆ABD và ∆ACE, ta có:
AD = AE (gt)
góc D = góc E (chứng minh trên)
DB = EC (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
b) Xét hai tam giác vuông BMD và CNE, ta có:
góc BMD=góc CNE=90o
BD = CE (gt)
góc D = góc E (chứng minh trên)
Suy ra: ∆BMD = ∆CNE (cạnh huyền, góc nhọn)
Suy ra: BM = CN (hai cạnh tương ứng)
c) Ta có: ∆BMD = ∆CNE (chứng minh trên)
Suy ra: góc DBM=góc ECN (hai góc tương ứng)
góc DBM=góc IBC (đối đỉnh)
góc ECN = góc ICB (đối đỉnh)
Suy ra: góc IBC=góc ICB hay ∆IBC cân tại I.
d) Xét ∆ABI và ∆ACI, ta có:
AB = AC (chứng minh trên)
IB = IC (vì ∆IBC cân tại I)
AI cạnh chung
Suy ra: ∆ABI = ∆ACI (c.c.c) ⇒ góc BAI=góc CAI (hai góc tương ứng)
Vậy AI là tia phân giác của góc BAC

tu ve hinh :
a, tamgiac ADE can tai A (gt)
=> AD = AE va goc ADE = goc AED (dn)
xet tamgiac ADB va tamgiac AEC co : DB = CE (gt)
=> tamgiac ADB = tamgiac AEC (c - g - c)
=> AB = AC (dn)
=> tamgiac ABC can tai A (dn)
b, xet tamgiac DMB va tamgiac ENC co :
goc DMB = goc ENC = 90o do MB | AD va CN | AE (gt)
goc ADE = goc AED (cau a)
DB = CE (gt)
=> tamgiac DMB = tamgiac ENC (ch - gn)
=> BM = CN (dn)

a) Vì tam giác ADE cân tại A nên: AD=AE; góc ADE= góc AED hay góc ADB= góc AEC
Xét tam giác ADB và tam giác AEC có:
DB=CE
góc ADB= góc AEC
AD=AE
Do đó: tam giác ADB= tam giác AEC (c.g.c)
=) AB=AC
=) tam giác ABC cân tại A
a) Vì tam giác ADE cân tại A nên AD=AE; góc ADE=góc AED hay góc ADB=góc AEC
Xét tam giác ADB và tam giác AEC có:
DB=EC(gt)
AD=AE(cmt)
Góc ADB=góc AEC
Suy ra tam giác ADB=tam giác AEC(c-g-c)
Suy ra AB=AC
Suy ra tam giác ABC cân tại A
k nha