Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi O là trung điểm của BC.
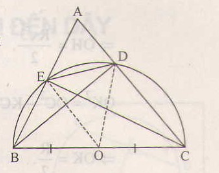
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
EO=12BC;DO=12BC.EO=12BC;DO=12BC.
Suy ra OE=OD=OB=OC(=12BC)OE=OD=OB=OC(=12BC)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường tròn nói ở câu a), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC.

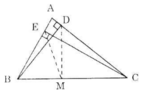
a) Gọi M là trung điểm của BC.

=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.

Lời giải chi tiết
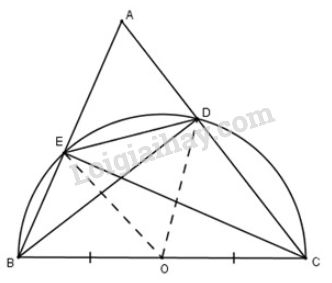
a) Gọi OO là trung điểm của BC⇒OB=OC=BC2.BC⇒OB=OC=BC2. (1)
Vì DODO là đường trung tuyến của tam giác vuông DBCDBC.
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
OD=12BCOD=12BC (2)
Từ (1) và (2) suy ra OD=OB=OC=12BCOD=OB=OC=12BC
Do đó ba điểm B, D, CB, D, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên OE=OB=OC=12BCOE=OB=OC=12BC
Suy ra ba điểm B, E, CB, E, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Do đó 4 điểm B, C, D, EB, C, D, E cùng thuộc đường tròn (O)(O) đường kính BCBC.
b) Xét đường (O;BC2)(O;BC2), với BCBC là đường kính.
Ta có DEDE là một dây cung không đi qua tâm nên ta có BC>DEBC>DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
a) Gọi \mathrm{M}M là trung điểm của \mathrm{BC}BC.
Ta có EM=\dfrac{1}{2} BC, DM=\dfrac{1}{2} BCEM=21BC,DM=21BC.
Suy ra ME=MB=MC=MDME=MB=MC=MD
do đó B, E, D, CB,E,D,C cùng thuộc đường tròn đường kính BCBC.
b) Trong đường tròn nói trên, DEDE là dây, BCBC là đường kính nên DE<BCDE<BC

1. Xét tam giác BEC vuông tại E có:
góc BEC = 90 độ
=> B,E,C thuộc vào đg tròn đg kính BC (1)
Xét tam giác BDC có
góc BDC = 90 độ
=> B, D, C thuộc đg tròn đg kính BC (2)
(1)(2)=> B, E, D, C thuộc vào cùng 1 đg tròn
2. Xét đường tròn tâm O có
CD là dây ( dựa vào 1)
Lai có I là trung điểm của CD
=> OI vuông góc với ED( đl )

a/ Ta có
\(BE\perp AC\Rightarrow\widehat{AEB}=90^o\)
\(AH\perp BC\Rightarrow\widehat{AHB}=90^o\)
=> E và H cùng nhìn AB dưới 1 góc bằng 90 độ => E;H,A;B thuộc đường tròn bán kính = \(\frac{AB}{2}\) , tâm là trung điểm AB
b/ Ta có
\(\widehat{DBE}=\widehat{DFE}\) (Góc nội tiếp đường tròn tâm O cùng chắn cung DE)
\(\widehat{DBE}=\widehat{AHE}\) (Góc nội tiếp đường tròn ngoại tiếp HBAE cùng chắn cung AE)
\(\Rightarrow\widehat{DFE}=\widehat{AHE}\) => DF//AH (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành hai góc ở vị trí đồng vị bằng nhau thì chúng // với nhau)
Mà \(AH\perp BC\Rightarrow DF\perp BC\)
c/
Từ E dựng đường thẳng vuông góc với BC cắt (O) tại I => gia của BC với EI là trung điểm EI (đường kính vuông góc với dây cung thì chia đôi dây cung) => I là điểm đối xứng E qua BC.
Nối I với H, D với H
Xét \(\Delta HDF\) và \(\Delta HEI\) ta có
\(BC\perp DF;BC\perp EI\) => BC đi qua trung điểm của DF và EI => tg HDF và tg HEI là tam giác cân tại H (có BC là đường cao đồng thời là đường trung trực)
\(\Rightarrow\widehat{HEI}=\widehat{HIE};\widehat{HDF}=\widehat{HFD}\) (góc ở đáy của tg cân)
Ta có DF//EI (cùng vuông góc với BC) => sđ cung DE = sđ cung FI (Trong đường tròn hai cung bị chắn bởi 2 dây // với nhau thì = nhau)
\(\Rightarrow\widehat{HFD}=\widehat{HEI}\) (góc nội tiếp cùng chắn 2 cung có số đo bằng nhau)
\(\Rightarrow\widehat{HEI}=\widehat{HIE}=\widehat{HDF}=\widehat{HFD}\) => tg HDF đồng dạng với tg HEI
\(\Rightarrow\frac{HD}{HE}=\frac{HF}{HI}\Rightarrow HD.HI=HE.HF\)

a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp