Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\overrightarrow{AB}=\overrightarrow{b}\), \(\overrightarrow{AC}=\overrightarrow{c}\)
Do B. M, C thẳng hàng theo thứ tự, nên tồn tại n, p > 0 sao cho \(\overrightarrow{AM}=n\overrightarrow{c}+p\overrightarrow{b}\) với \(n+p=1\)
Từ đó, do tứ giác ANMP là hình bình hành, nên \(\overrightarrow{AP}=p\overrightarrow{b}\), \(\overrightarrow{AN}=n\overrightarrow{c}\)
Do B, O, N thẳng hàng và C, O, P thẳng hàng nên
\(\overrightarrow{AO}=x\overrightarrow{b}+ny\overrightarrow{c}=z\overrightarrow{c}+pt\overrightarrow{b}\)
trong đó \(x+y=1=z+t\)
Từ đó, do hai vectơ \(\overrightarrow{b},\overrightarrow{c}\) không cùng phương nên \(x=\frac{p\left(1-n\right)}{1-np}\) và \(y=\frac{1-p}{1-np}\)
Do đó :
\(\overrightarrow{AO}=\frac{p\left(1-n\right)}{1-np}.\overrightarrow{b}+\frac{n\left(1-p\right)}{1-np}.\overrightarrow{c}\)
Suy ra :
\(\left(1-np\right).\overrightarrow{OM}=\left(1-np\right)\left(\overrightarrow{AM}-\overrightarrow{AO}\right)=np\left(1-p\right)\overrightarrow{b}+np\left(1-n\right)\overrightarrow{c}\)
\(\Rightarrow\frac{1-np}{np}.\overrightarrow{OM}=\left(\overrightarrow{b}+\overrightarrow{c}\right)-\left(n\overrightarrow{c}+p\overrightarrow{b}\right)\)
Hay
\(\overrightarrow{AM}=np\overrightarrow{AD}+\left(1-np\right)\overrightarrow{AO}\)
Trong đó D là điểm thỏa mãn \(\overrightarrow{AD}=\overrightarrow{b}+\overrightarrow{c}\) Từ đó, đường thẳng OM luôn đi qua D cố định (D là đỉnh thứ tư của hình bình hàng ABDC)

Đáp án A
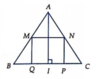
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
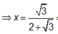
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì
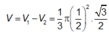
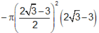
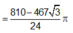

a.
Trong mp (SAB), nối MN kéo dài cắt AB tại E
\(\Rightarrow\left\{{}\begin{matrix}E\in\left(MNP\right)\\E\in\left(ABCD\right)\end{matrix}\right.\)
Mặt khác theo giả thiết \(\left\{{}\begin{matrix}P\in\left(ABCD\right)\\P\in\left(MNP\right)\end{matrix}\right.\)
\(\Rightarrow EP=\left(MNP\right)\cap\left(ABCD\right)\)
b.
Theo giả thiết: \(\left\{{}\begin{matrix}M\in\left(MNP\right)\\M\in SA\Rightarrow M\in\left(SAD\right)\end{matrix}\right.\)
Trong mp (ABCD), nối EP kéo dài cắt AD tại F
\(\Rightarrow\left\{{}\begin{matrix}F\in\left(MNP\right)\\F\in\left(SAD\right)\end{matrix}\right.\)
\(\Rightarrow MF=\left(MNP\right)\cap\left(ABCD\right)\)
c.
Trong mp (SBC), nối NP kéo dài cắt SC tại H
\(\Rightarrow\left\{{}\begin{matrix}H\in\left(MNP\right)\\H\in\left(SCD\right)\end{matrix}\right.\)
Gọi giao điểm của EP và CD tại K
\(\Rightarrow HK=\left(MNP\right)\cap\left(SCD\right)\)

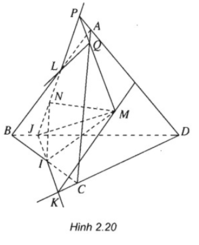
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
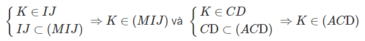
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
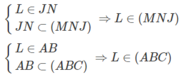
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
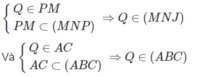
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).

+) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Từ đó suy ra: IJ // BC (3) .
- Từ (1) và (3) suy ra: MN // IJ .
→ Vậy tứ giác MNJI là hình thang.
+) Để MNJI là hình bình hành thì: MI// NJ.
- Lại có ba mặt phẳng (MNJI); (ABD); (ACD) đôi một cắt nhau theo các giao tuyến là MI, NJ, AD nên theo định lý 1 ta có: MI // AD // NJ (4)
- Mà I; J lần lượt là trung điểm BD,CD (5)
- Từ (4)và (5) suy ra: M, N lần lượt là trung điểm của AB, AC.
⇒ Vậy điều kiện để hình thang MNJI trở thành hình bình hành là M, N lần lượt là trung điểm của AB, AC.

Đáp án D.
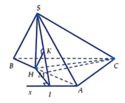
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
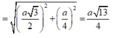
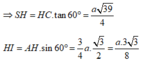
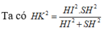
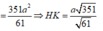
![]()
![]()



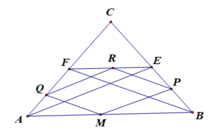
Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh
O A P B N C D M