Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
=>BA=BM
Xét ΔBME vuông tại M và ΔBAC vuông tại A có
BM=BA
góc MBE chung
=>ΔBME=ΔBAC
=>BE=BC
=>ΔBEC cân tại B
b: Xét ΔDAE vuông tại A và ΔDMC vuông tại M co
DA=DM
góc ADE=góc MDC
=>ΔDAE=ΔDMC
=>DE=DC
=>D nằm trên trung trực của EC
mà BK là trung trực của EC
nên B,D,K thẳng hàng

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC>DE

Ta có hình vẽ:
A B C D E
Xét hai tam giác vuông ABD và EBD có:
BD: cạnh chung
góc ABD = góc EBD
=> tam giác ABD = tam giác EBD
=> AB = BE (hai cạnh tương ứng)

\(\text{#TNam}\)
`a,` Xét Tam giác `ABD` và Tam giác `EBD` có:
`\text {BD chung}`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\)\(\widehat{BAE})\)
`=> \text {Tam giác ABD = Tam giác EBD (ch-gn)}`
`b,`
Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> BA = BE (\text {2 cạnh tương ứng})`
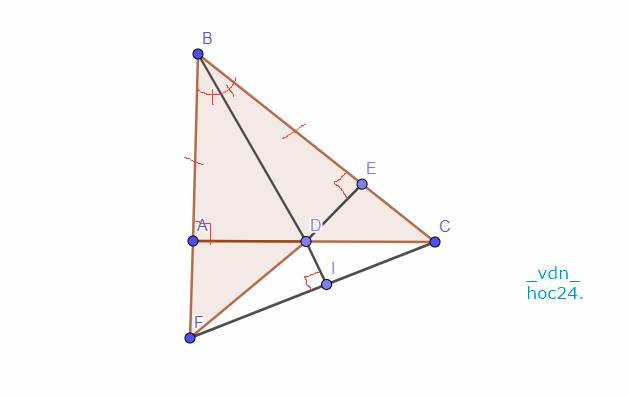
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{B}\) \(\text {chung}\)
`BA = BE (CMT)`
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Gọi `I` là giao điểm của `BD` và `CF`
Xét Tam giác `BIF` và Tam giác `BIC` có:
`BF = BC (CMT)`
\(\widehat{FBI}=\widehat{CBI} (\text {tia phân giác}\) \(\widehat{FBC})\)
\(\text {BI chung}\)
`=> \text {Tam giác BIF = Tam giác BIC (c-g-c)}`
`->`\(\widehat{BIF}=\widehat{BIC} (\text {2 góc tương ứng})\)
Mà `2` gióc này nằm ở vị trí kề bù
`->`\(\widehat{BIF}+\widehat{BIC}=180^0\)
`->`\(\widehat{BIF}=\widehat{BIC}=\)`180/2=90^0`
`-> \text {BI} \bot \text {FC}`
`-> \text {BD}` `\bot` `\text {FC (đpcm)}`

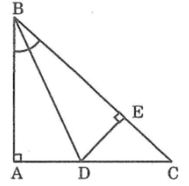
Xét hai tam giác vuông ABD và EBD, ta có:
∠(BAD) =∠(BED) =90o
Cạnh huyền BD chung
∠(ABD) =∠(EBD) (Do BD là tia phân giác của góc ABC)
Suy ra: Δ ABD= Δ EBD(cạnh huyền, góc nhọn)
Vậy BA = BE ( hai cạnh tương ứng)

hình tự vẽ: Xét t/g ABD và t/g BDE có:
góc ABD= góc DBE (gt)
góc A= góc E (=90o)
BD là cạnh chung
\(\Rightarrow\)T/g ABD= t/g BDE ( cạnh huyền-góc nhọn )
\(\Rightarrow\)AB=BE (hai cạnh tương ứng ).

