Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
hihihihihihiihiihiihihiihihihihihihihihihihihihihihiihihiihihihihihihiihihihihihihihihihihihihihihihihhihihihihihihihhiihihihihihiihihiihihihihihihihihihihihihihihihihiihihihihihiihihihihihihihihihiihihihihiihiihihihihiihihihihihiihihihihihiihhiihihihiihihihihihiihihihihhiihhiihiihihihihihihihihihihihiihhiiihhiihhiihihihihihihihiihihih

Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath

Cách làm :
Bạn chỉ cần chứng minh AEDM là HCN ;O là trung điểm của DE =>O cũng là trung điểm của AM =>O,M,A thẳng hàng
b,
Gọi P ,Q lần lượt là trung điểm của AB,AC
=> giới hạn :
*Khi M trùng với B=> O trùng với P
*Khi M trùng với C=> O trùng với Q
=> I thuộc PQ
c,
Kẻ đường cao AH
Khi M trùng với H thì AM ngắn nhất (quan hệ đường vuông góc và đường xiên)

Bài giải:
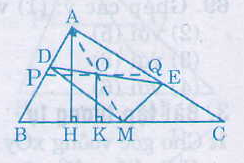
a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.

a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.
=
Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Chú ý rằng: EF//BC, EF, BC đều cố định nên khoảng cách giữa 2 đường thẳng này là cố định.
Vậy thì I luôn cách BC một khoảng cố định.