Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên AM=1/2BC

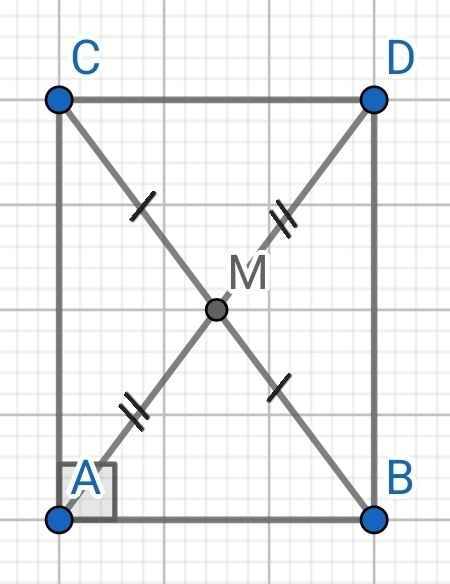
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC

Bn tự vẽ hình nha!!!
a) Xét \(\Delta ABM\) và \(\Delta DCM\) có:
MB = MC (M là trung điểm BC (gt))
\(\widehat{AMB} = \widehat{DMC}\)(đối đỉnh)
MA = MD (gt)
\(\Rightarrow\)\(\Delta ABM = \Delta DCM (cgc)\)
b) Vì \(\Delta ABM = \Delta DCM (cmt)\)
\(\Rightarrow\)\(\widehat{BAM} = \widehat{CDM}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\) AB // CD
c) Vì \(\Delta ABM = \Delta DCM (cmt)\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
MA=MD
Do đó: ΔMBA=ΔMCD

a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét ΔMEB và ΔMFC có
ME=MF
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMEB=ΔMFC
=>\(\widehat{MEB}=\widehat{MFC}\)
=>\(\widehat{MFC}=90^0\)
=>CF\(\perp\)AD
c: Xét tứ giác BFCE có
M là trung điểm chung của BC và FE
=>BFCE là hình bình hành
=>BF//CE và BF=CE
Ta có: BF//CE
B\(\in\)FG
Do đó: BG//CE
Ta có: BF=CE
BF=BG
Do đó: BG=CE
Xét tứ giác BGEC có
BG//EC
BG=EC
Do đó: BGEC là hình bình hành
=>BE cắt GC tại trung điểm của mỗi đường
mà H là trung điểm của BE
nên H là trung điểm của GC
=>G,H,C thẳng hàng

a, Xét △BMA và △CMD
Có: MB = MC (gt)
BMA = CMD (2 góc đối đỉnh)
MA = MD (gt)
=> △BMA = △CMD (c.g.c)
=> MBA = MCD (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AB // CD (dhnb)
Mà AB ⊥ AC (gt)
=> CD ⊥ AC (từ vuông góc đến song song)
Xét △ABC vuông tại A và △CDA vuông tại C
Có: AC là cạnh chung
AB = DC (△BMA = △CMD)
=> △ABC = △CDA (2cgv)
b, △ABC = △CDA (cmt)
=> BC = AD (2 cạnh tương ứng)
=> BC = 2AM
=> AM = BC : 2
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên AM=BC/2