Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tg vuông AHB~AHC => AH/BH=CH/AH=AC/AB
nhưng AH=2HM ; BH=2HN -gt- nên AV/BH=..=AC/AB=HM / HN
do đo ta có hai tg vuông CHM & AHN cũng ~ với nhau ( ~ là đồng dạng)
suy ra góc ^HAN=^HCM<=> CM và AN là hai cạnh tương ứng của hai góc =mà cặp cạnh kia CH đã vuông góc vơi AH
hoặc MN//AB ta cứ cộng các góc(=) dồn lại cũng ra ^NCM+^MNC+^MNA=!V

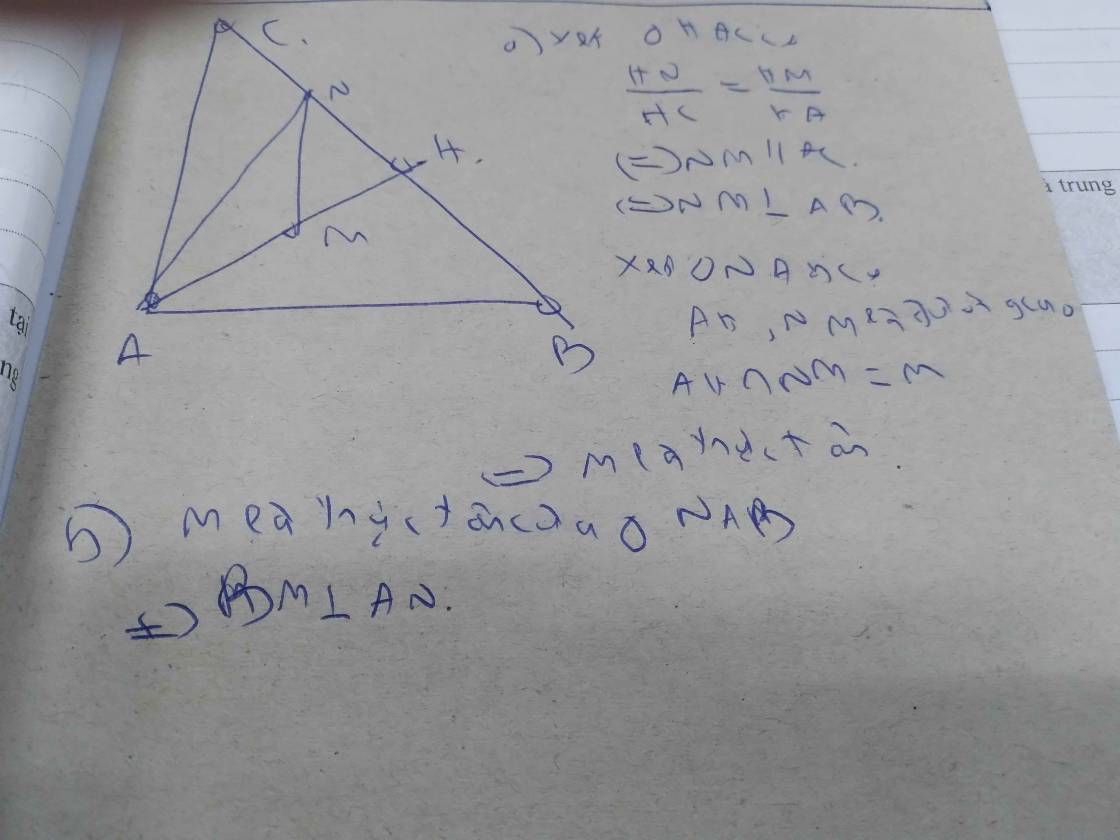
Hình:
M N A B C H
Giải:
a) Ta có:
M là trung điểm của AH
N là trung điểm của CH
⇒ MN là đường trung bình của tam giác AHC
\(\Rightarrow MN//AC\) (Tính chất của đường trung bình)
Mặt khác: \(AC\perp AB\)
\(\Rightarrow MN\perp AB\)
⇒ M là giao điểm của hai đường cao AH và MN
⇒ M là trực tâm của tam giác ANB
b) Vì M là trực tâm của tam giác ANB (câu a)
=> BM là đường cao của tam giác ANB
\(\Rightarrow BM\perp AN\)
Vậy ...