Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
\(ME\perp AB;AC\perp AB\) => ME//AC
\(MF\perp AC;AB\perp AC\) => MF//AB
=> AEMF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh
Mà \(\widehat{BAC}=90^o\)
=> AEMF là HCN (Hình bình hành có 1 góc vuông là HCN)
b/
Ta có E; F; H cùng nhìn AM dưới một góc vuông => E; F; H cùng nằm trên đường tròn đường kính AM tâm là trung điểm AM
Mà AM=EF (Trong HCN hai đường chéo bằng nhau) => EF cũng là đường kính của đường tròn đường kính AM
\(\Rightarrow\widehat{EHF}=90^o\Rightarrow HE\perp HF\) (góc nội tiếp chắn nửa đường tròn)

Bạn tự vẽ hình nhé!
a) Xét tứ giác HFAEHFAE có HFAˆ=FAEˆ=AEHˆ=900HFA^=FAE^=AEH^=900 nên HFAEHFAE là hình chữ nhật.
Do đó:
AFEˆ=900−EFHˆ=900−HAEˆ=900−(900−BAHˆ)AFE^=900−EFH^=900−HAE^=900−(900−BAH^)
=BAHˆ=900−Bˆ(1)=BAH^=900−B^(1)
Tam giác ABCABC vuông có MM là trung điểm cạnh huyền nên AM=BC2=BMAM=BC2=BM
⇒△AMB⇒△AMB cân tại MM
⇒Bˆ=MBAˆ=MABˆ(2)⇒B^=MBA^=MAB^(2)
Từ (1);(2)⇒AFEˆ=900−MABˆ(1);(2)⇒AFE^=900−MAB^
⇔AFEˆ+MABˆ=900⇔AFE^+MAB^=900
⇒EF⊥AM⇒EF⊥AM
b) Sửa lại đề: EF∥BDEF∥BD
Tam giác BACBAC có MM là trung điểm BCBC, NN là trung điểm ABAB nên MNMN là đường trung bình của tam giác ABCABC. Do đó MN∥ACMN∥AC. Mà AB⊥AC⇒MN⊥ABAB⊥AC⇒MN⊥AB
Ta thấy tam giác BAMBAM có AH⊥BM,MN⊥BAAH⊥BM,MN⊥BA và AH∩MN=DAH∩MN=D nên DD là trực tâm tam giác BAMBAM
Do đó: BD⊥AMBD⊥AM. Mà EF⊥AM⇒BD∥EF

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: BC=10cm
AH=4,8cm
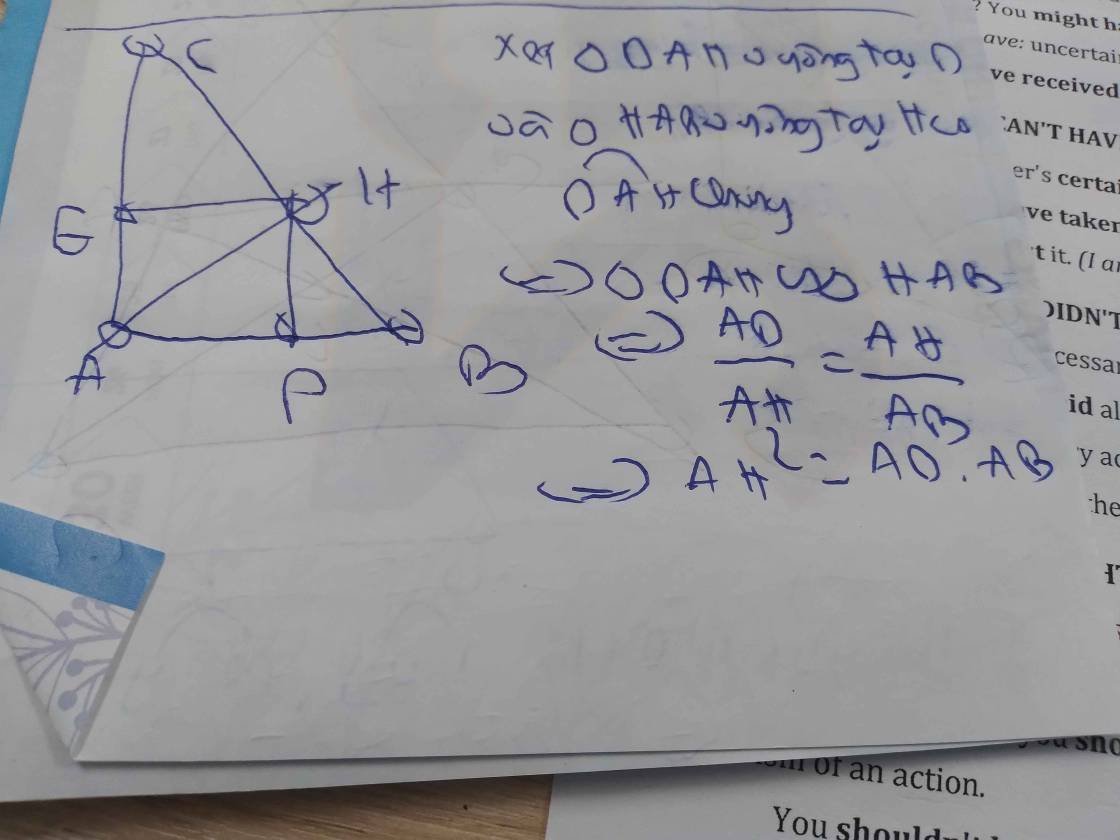
c: Xét ΔABH vuông tại H có HM là đườg cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
\(a)\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\\ \widehat{ABC}chung.\\ \Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b)\) Xét \(\Delta ABC\) vuông tại A:
\(+)BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=6^2+8^2=36+64=100.\\ \Rightarrow BC=10\left(cm\right).\)\(+)AH.BC=AB.AC\) (Hệ thức lượng).\(\Rightarrow AH.10=6.8.\\ \Rightarrow AH=4,8\left(cm\right).\)\(c)\) Xét \(\Delta ABH\) vuông tại H, đường cao MH:\(AH^2=AM.AB\) (Hệ thức lượng). \(\left(1\right)\)Xét \(\Delta ACH\) vuông tại H, đường cao NH:\(AH^2=AN.AC\) (Hệ thức lượng). \(\left(2\right)\)Từ \(\left(1\right);\left(2\right)\Rightarrow AM.AB=AN.AC.\)Xét \(\Delta ACB\) và \(\Delta AMN:\)\(\Rightarrow\dfrac{AB}{AN}=\dfrac{AC}{AM}.\)\(\widehat{A}chung.\\ \dfrac{AB}{AN}=\dfrac{AC}{AM}\left(cmt\right).\\ \Rightarrow\Delta ACB\sim\Delta AMN\left(c-g-c\right).\)