Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)


a)Ta có:BD=BA(gt)
⇒ΔBAD cân tại B
⇒góc BAD=góc BDA
Trong ΔADH vuông tại H,có:
góc DAH+góc ADH=90 độ
Mà góc BAD+góc DAK=90 độ
⇒DAH+ADH=BAD+DAK
Mà góc ADH=góc BAD(cmt)
⇒Góc DAH=góc DAK
⇒AD là tia phân giác của góc HAC
b)Xét ΔADH và ΔADK,có:
góc H=góc K=90 độ
AD chung
góc DAH=góc DAK
⇒ΔADH=ΔADK(ch-gn)
⇒AH=AK(2 cạnh t/ứ)
c)Ta có:KC<DC(ΔKDC vuông tại K)
Mà KC=AC-AK
DC=BC-BD
⇒AC-AK<BC-BD
⇒ AC + BD < BC + AK
Mà BD=BA(gt)
⇒AK = AH (cmt)
⇒AB+AC<BC+AH
#Cừu
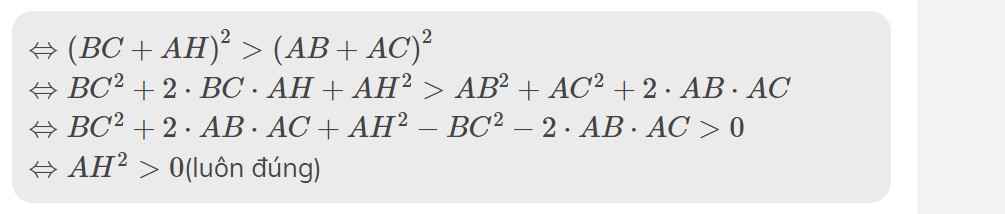
Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).