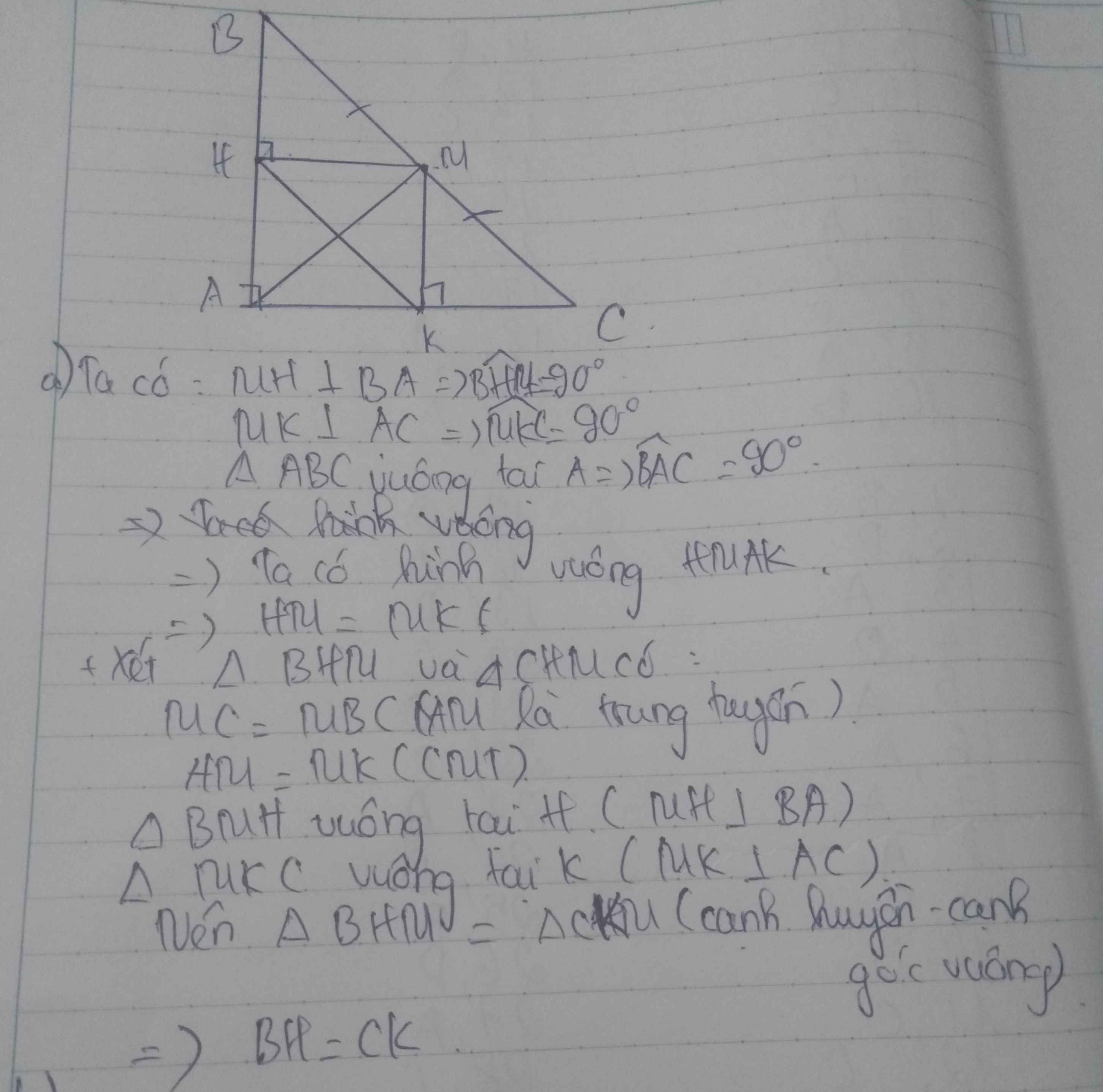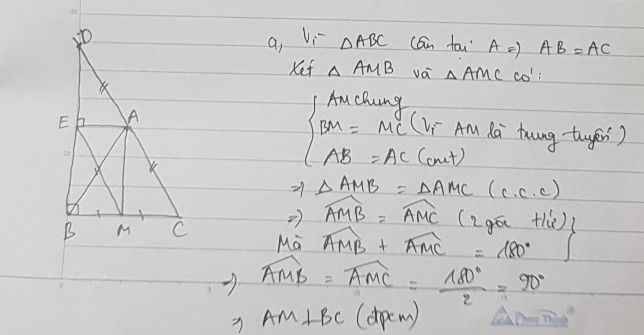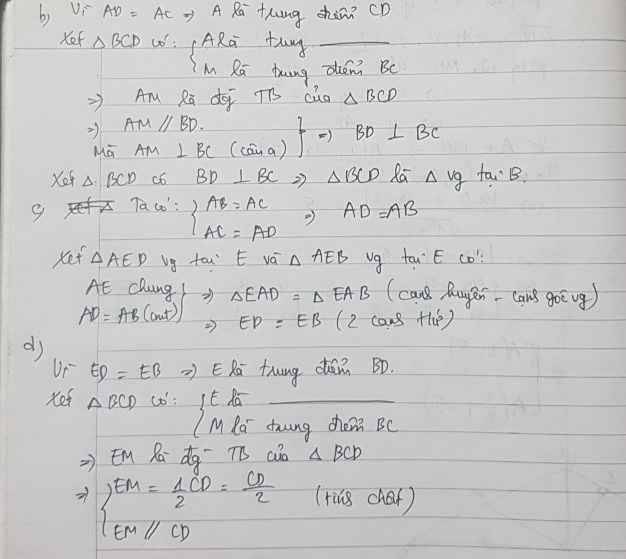Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a./ \(\Delta BEM=\Delta CFM\)vì:
- góc BEM = góc CFM ( = 90o )
- góc EBM = góc FCM (2 góc bằng nhau của tam giác cân ABC tại A)
- => góc EMB = góc FMC ( = 180o - 2 góc bằng nhau)
- MB = MC (vì AM là trung tuyến).
b./ => ME = MF (cạnh tương ứng của 2 tam giác bằng nhau) => M nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (1)
\(\Delta BEM=\Delta CFM\)=> BE = CF => AE = AF ( vì cùng bằng AB - BE = AC - CF)
=> A nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (2)
Từ (1) (2) => AM là trung trực của EF.

$BH=\frac{AB}{2}; CK=\frac{AC}{2}$ nên nếu $BH=CK$ thì $AB=AC$. Điều này không có trong điều kiện đề bài.
Bạn xem lại đề.

b) ta có tam giác ABC cân
=> \(\widehat{B}=\widehat{C}=180-\widehat{A}\) (1)
mà AM là trung tuyến => AM cx là phân giác và AM cx là đường cao (t/c tam giác cân)
=>\(\widehat{A1}=\widehat{A2}\)
xét tam giác AEM và tam giác AfM
có AM chung
\(\widehat{E}=\widehat{F}\)=90o
\(\widehat{A1}=\widehat{A2}\)
=> tam giác AEM =tam giác AFM (CH-GN)
=> AE =AC (2 cạnh tương ứng)
=> tam giác AEF cân ở \(\widehat{A}\)
=> \(\widehat{E}=\widehat{F}=180-\widehat{A}\) (2)
từ 1 và 2 =>\(\widehat{E}=\widehat{B}\) mà 2 góc ở vt đồng vị
=> EF // BC
mà AM ⊥ BC
=> EF ⊥ AM
=> AM là trung trực của EF (t/c tam giác cân)

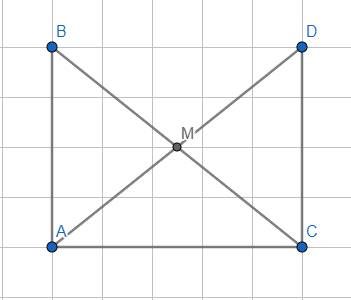
a, Có: AM là trung tuyến ΔABC
\(\Rightarrow\) M là trung điểm BC
\(\Rightarrow MB=MC\)
Xét ΔABM và ΔCDM có:
\(MB=MC\left(cmt\right)\)
\(\widehat{AMB}=\widehat{CMD}\left(đ^2\right)\)
\(MA=MD\)
\(\Rightarrow\) ΔABM = ΔCDM ( c.g.c )
\(\Rightarrow\widehat{BAM}=\widehat{DCM}\left(2gtu\right)\)
\(\Rightarrow AB//CD\)
Mà \(BA⊥AC\)
\(\Rightarrow DC⊥AC\)
b, Có: ΔABM = ΔCDM ( cmt )
\(\Rightarrow\left\{{}\begin{matrix}BA=DC\left(2ctu\right)\\\widehat{ABM}=\widehat{CDM}\left(2gtu\right)\end{matrix}\right.\)
Xét ΔABC và ΔCDA có:
\(\widehat{ABM}=\widehat{CDM}\left(cmt\right)\)
\(AB=CD\left(cmt\right)\)
\(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\)
\(\Rightarrow\) ΔABC = ΔCDA ( g.c.g )
\(\Rightarrow BC=DA\left(2ctu\right)\)
Có: M là trung điểm BC
M là trung điểm AD ( MA = MD )
Mà \(BC=AD\)
\(\Rightarrow MA=MB\)
\(\Rightarrow\) ΔABM cân tại M
Mà \(\widehat{ABM=60^o}\)
\(\Rightarrow\) ΔABM là tam giác đều.

ABCNM
a ) Xét tam giác AMB và tam giác NMC có :
AM = MN ( gt )
Góc AMB = góc NMC ( đối đỉnh )
BM = MC ( vì AM là đường trung tuyến của BC )
=> Tam giác AMB = Tam giác NMC ( c.g.c )
=> Góc ABM = góc NCM ( 2 góc tương ứng )
Mà góc ABM = góc NCM so le trong
=> CN // AB
b ) Xét tam giác ABC và tam giác NCB có :
AB = NC ( tam giác AMB = tam giác NMC mà cạnh AB và NC là 2 cạnh tương ứng )
Góc ABC = góc NCB ( vì tam giác AMB = tam giác NMC mà góc ABC và góc NCB là 2 góc tương ứng )
AB là cạnh chung
=> Tam giác ABC = Tam giác NCB ( c.g.c )

a: ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
b: Xét ΔDBC có
BA là trung tuyến
BA=CD/2
=>ΔDBC vuông tại B
c: ΔABD cân tại A có AE là đường cao
nên E là trung điểm của BD
d: Xét ΔDBC có BE/BD=BM/BC
nên EM//DC