Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BCEDAF
*Hình quên đánh dấu ABD = DBE nhé
*Cần viết gt và kl thì bảo mình nhá <3
Giải
a) Xét ∆ABD và ∆EBD có :
AB = BE (gt) |
FBD = DBE (AD là tia phân giác ABE) }
BD là cạnh chung |
=> ∆ABD = ∆EBD (c.g.c)

B E C A D F
Xét \(\Delta ABD\) và \(\Delta EBD\)
ta có DA = DE ( gt )
BA = BE ( gt )
BD là cạnh chung
=> \(\Delta ABD=\Delta EBD\left(c.c.c\right)\)

A)Xét tam giác ABD và EBD
DB chung
\(\widehat{EBD}=\widehat{DBA}\)
AB=AE
=> tam giác ABD = tam giác EBD
B)DE=AD
DE\(⊥\)BC
Xét tam giác vuông DEC và DAM
\(\widehat{CDE}=\widehat{MDA}\)
AD=DE
=> tam giác ADM = tam giác EDC => CE =AM
C) MÌNH KO BIẾT

Xét ΔABDΔABD và ΔEBDΔEBD, ta có:
AB=BE ( gt)
ABDˆ=EBDˆABD^=EBD^ ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD⇒ΔABD=ΔEBD (c-g-c)

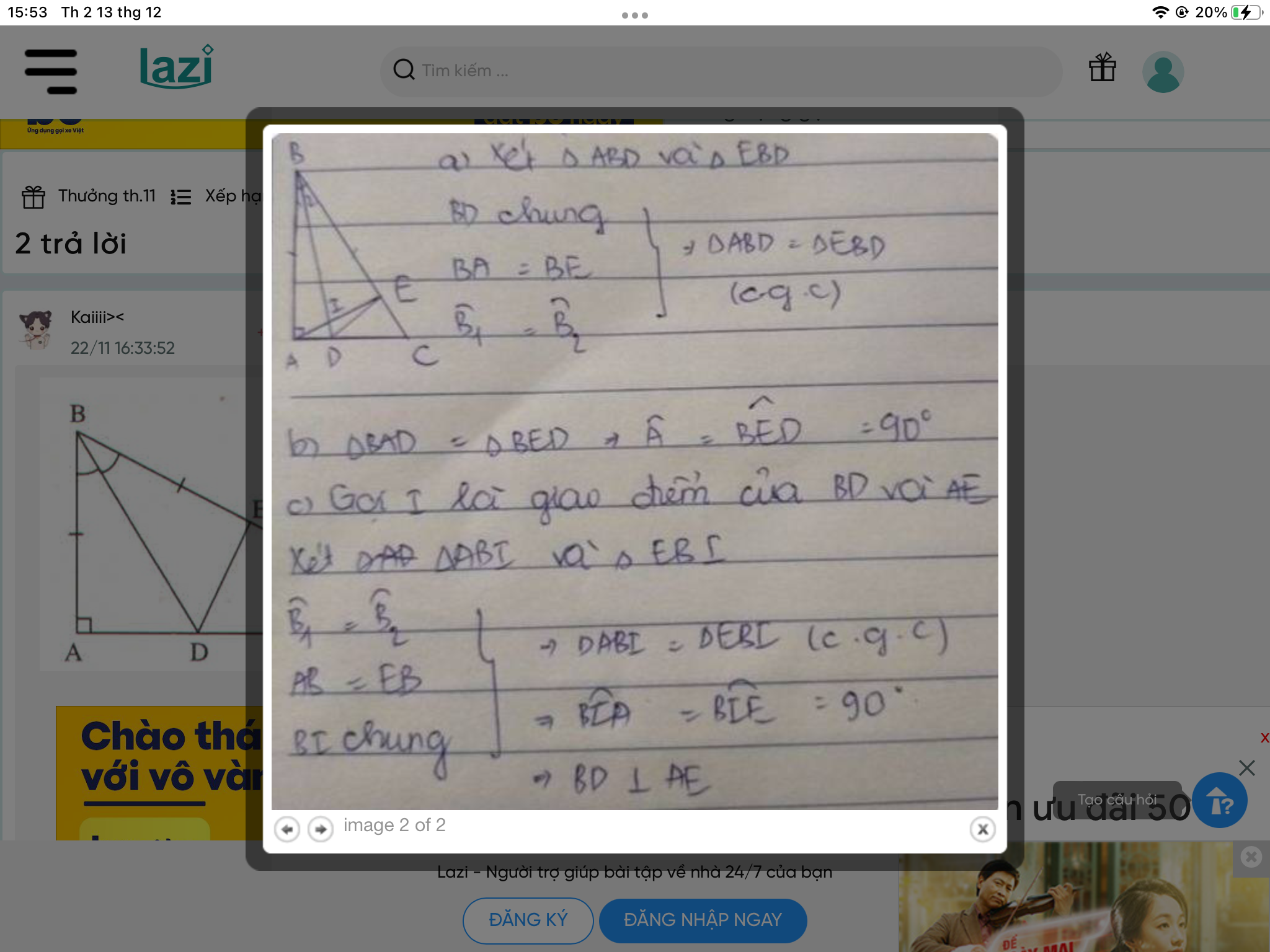
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

đố các bạn
bé kia chăn vịt khác thường
buộc đi cho được chẵn hàng mới ưa
hàng 2 xếp thấy chưa vừa,
hàng 3 xếp vẫn còn thừa 1 con,
hàng 4 xếp vẫn chưa tròn,
hàng 5 xếp thiếu 1 con mới đầy
xếp thành hàng 7, đẹp thay!
vịt bao nhiêu ? tính được ngay mới tài !

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF