Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

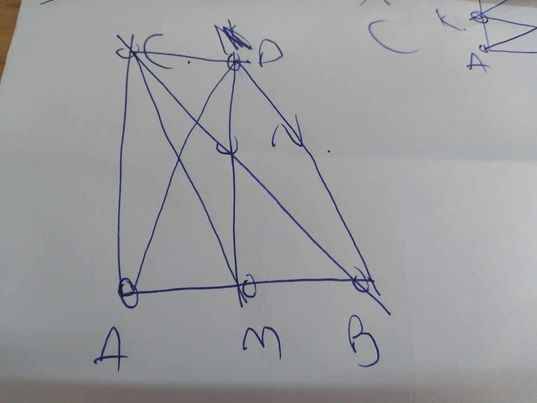
a: Xét tứ giác BMCD có
N là trung điểm chung của BC và MD
=>BMCD là hình bình hành
b: Ta có: BMCD là hình bình hành
=>BM//CD và BM=CD
Ta có: BM//CD
M\(\in\)AB
Do đó: AM//CD
ta có: BM=CD
AM=MB
Do đó: AM=CD
Xét tứ giác AMDC có
AM//DC
AM=DC
Do đó: AMDC là hình bình hành
Hình bình hành AMDC có \(\widehat{MAC}=90^0\)
nên AMDC là hình chữ nhật
c: Ta có: AMDC là hình chữ nhật
=>\(\widehat{DMA}=90^0\)
=>DM\(\perp\)AB tại M
Xét ΔDBA có
DM là đường cao
DM là đường trung tuyến
Do đó: ΔDBA cân tại D

a: Xét tứ giác AIMJ có
\(\widehat{AIM}=\widehat{AJM}=\widehat{JAI}=90^0\)
=>AIMJ là hình chữ nhật
b: AIMJ là hình chữ nhật
=>MI//AJ và MI=AJ
MI=AJ
MN=MI
Do đó: MN=AJ
MI//AJ
N\(\in\)MI
Do đó: MN//JA
Xét tứ giác AMNJ có
AJ//MN
AJ=MN
Do đó: AMNJ là hình bình hành

a: Xét ΔABC có
E là trung điểm của BC
F là trung điểm của CA
Do đó: EFlà đường trung bình
=>EF//AB và EF=AB/2(1)
Xét ΔABD có
H là trung điểm của DB
G la trung điểm của AD
Do đó: HG là đường trung bình
=>HG//AB và HG=AB/2(2)
Từ (1) và (2) suy ra HG//FE và HG=FE
b: HE=DC/2
EF=AB/2
mà AB=DC
nên HE=FE
Xét tứ giác EFGH có
EF//GH
EF=GH
Do đó: EFGH là hình bình hành
mà EH=EF
nên EFGH là hình thoi

1:
ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
EH\(\perp\)BC tại H
=>EH\(\perp\)HB tại H
=>ΔEHB vuông tại H
Xét ΔHEB vuông tại H có \(\widehat{HBE}=45^0\)
nên ΔHEB vuông cân tại H
FG\(\perp\)BC tại G
=>FG\(\perp\)GC tại G
=>ΔFGC vuông tại G
Xét ΔFCG vuông tại G có \(\widehat{GCF}=45^0\)
nên ΔFCG vuông cân tại G
2: EH\(\perp\)BC
FG\(\perp\)BC
Do đó: EH//FG
EH=HB
HB=HG=GC
GF=GC
Do đó; EH=HB=GH=CG=GF
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHFG là hình bình hành
Hình bình hành EHFG có \(\widehat{EHG}=90^0\)
nên EHFG là hình chữ nhật
Hình chữ nhật EHFG có GH=GF
nên EHFG là hình vuông

a: \(NP\perp BC;MQ\perp BC\)
Do đó: NP//MQ
ΔMQB vuông tại M có \(\widehat{B}=45^0\)
nên ΔMQB vuông cân tại M
=>MQ=MB
ΔNPC vuông tại N có \(\widehat{C}=45^0\)
nên ΔNPC vuông cân tại N
=>NP=NC
NP=NC
MQ=MB
NC=MB
Do đó: NP=MQ
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
Do đó: MNPQ là hình bình hành
mà \(\widehat{PNM}=90^0\)
nên MNPQ là hình chữ nhật
b: Để MNPQ là hình vuông thì QM=MN
=>MB=MN
=>\(MB=MN=NC\)
=>\(MN=\dfrac{BC}{3}\)
Vậy: M,N nằm trên đoạn BC sao cho \(CN=NM=MB=\dfrac{CB}{3}\) thì MNPQ là hình vuông

a/
��⊥��ME⊥AB (gt)
��⊥��⇒��⊥��AC⊥AB⇒AF⊥AB
=> ME//AF
��⊥��⇒��⊥��AB⊥AC⇒AE⊥AC
=> MF//AE
=> AEMF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có �^=90�A=90o
=> AEMF là HCN (hbh có 1 góc vuông là HCN)
b/
Ta có
MF
Xét tg vuông ABC có
MB=MC (gt); MF//AE => MF//AB
=> AF=BF (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
MF=IF (gt)
=> AMCI là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
��⊥��⇒��⊥��MF⊥AC⇒MI⊥AC
=> AMCI là hình thoi (hbh có 2 đường chéo vuông góc là hình thoi)
c/
Ta có
AI//CM (cạnh đối hình thoi) => AI//BC => ABCI là hình thang
Xét tứ giác ABMI có
AI//BC (cmt) => AI//BM
MF//AB (cmt) => MI//AB
=> ABMI là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Để ABCI là hình thang cân => AB=CI (1)
Ta có
AB=MI (cạnh đối hình bình hành ABMI) (2)
AM=CI (cạnh đối hình thoi AMCI) (3)
Từ (1) (2) (3) => AB=AM=MI=CI
Xét tg vuông ABC có
BM=CM ⇒��=��=��=��2⇒AM=BM=CM=2BC (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> AB=AM=BM => tg ABM là tg đều ⇒�^=60�⇒B=60o
Để ABCI là hình thang cân thì tg vuông ABC có �^=60�B=60o
d/
Xét tứ giác ADBM có
DE=ME (gt)
AE=BE (gt)
=> ADBM là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//BM (cạnh đối hbh) => AD//BC
Ta có
AI//CM (cạnh đối hình thoi AMCI)
=> A;D;I thẳng hàng (từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
Ta có
AD=BM (cạnh đối hbh ADBM)
AI=CM (cạnh đối hình thoi AMCI)
BM=CM (gt)
=> AD=AI => A là trung điểm DI
chúc bạn học tốt