Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Đề hay quá!)
Gọi \(X\) là trung điểm \(BC\). CM được \(DF,AI,MN\) đồng quy tại điểm ta gọi là \(K\).
Theo tính chất đường trung bình ta có \(MN\) song song \(AB\).
Do tam giác \(ABC\) vuông tại \(A\) cũng suy ra \(AB\) song song với \(IE\).
Áp dụng định lí Thales liên tục ta có:
\(\frac{AN}{IE}=\frac{MN}{MI}=\frac{KA}{KI}=\frac{AP}{ID}\).
Do \(ID=IE\) nên \(AN=AP\). Kết thúc chứng minh.

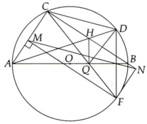
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!
Thực ra nó đúng với mọi tam giác \(ABC\) chứ không cần phải vuông đâu.
A B C D F M X K I
Ta vẽ \(CK⊥AI\) tại \(K\).
Bước 1: CM \(K,M,X\) thẳng hàng.
Do \(KM\) là trung tuyến của tam giác vuông \(AKC\) nên \(\widehat{KMC}=2\widehat{KAC}=\widehat{BAC}\).
Tức là \(KM\) song song với \(AB\).
Lại thêm \(MX\) song song với \(AB\) nên theo tiên đề Euclide thì \(K,M,X\) thẳng hàng.
Bước 2: CM \(K,D,F\) thẳng hàng.
\(IDKC\) nội tiếp nên \(\widehat{KDC}=\widehat{KIC}=\frac{1}{2}\left(\widehat{BAC}+\widehat{C}\right)=\frac{1}{2}\left(180^o-\widehat{B}\right)=\widehat{FDB}\)
(Dấu bằng cuối cùng là do tam giác \(FDB\) cân tại \(B\)).
Từ \(\widehat{KDC}=\widehat{FDB}\) chứng minh được \(K,D,F\) thẳng hàng.
Vậy \(DF,AI,MX\) đồng quy.