Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

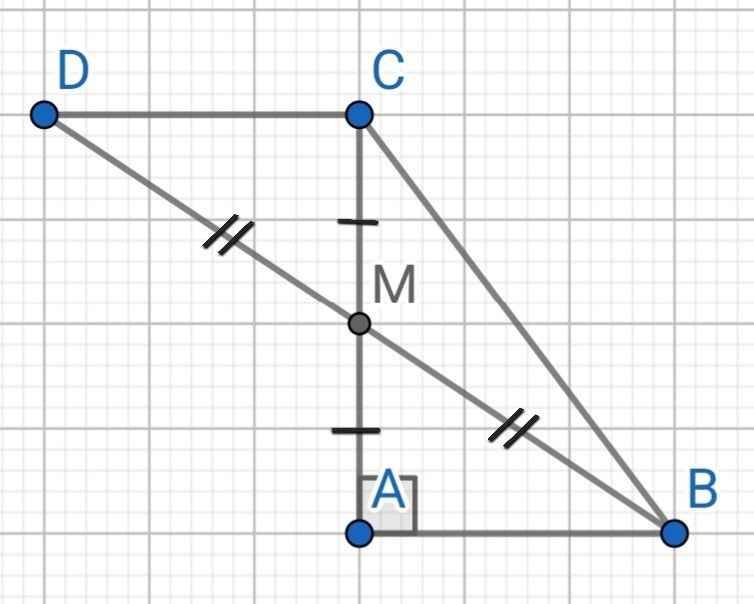 a) Xét ∆ABM và ∆CDM có:
a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD

TL:
1) Xét tam giác ABM và tam giác CDM có:
- AM = CM
- Góc AMB = góc CMD (2 góc đối đỉnh)
- BM = DM
-> Tam giác ABM = tam giác CDM (c.g.c)
2) Vì tam giác ABM = tam giác CDM
-> Góc MAB = góc MCD = 90o
-> MC vuông góc vs CD hay AC vuông góc vs DC
3) Vì E là trung điểm của BC , M là trung điểm của AC -> EM là đường trung trực của tam giác ABC -> EM//AB mà AB//DC (cùng vuông góc với AC) nên EM//DC hay MF//DC, ta có:
- M là trung điểm của AC (giả thiết)
- MF//DC (cmt)
Nên MF là đường trung trực của tam giác ACD
-> F là trung điểm của AD
EM RẢNH NÊN EM MỚI TL CHỨ LÂU NHƯ NÀY EM KO RẢNH CHẮC KO TL ĐÂU
TL:
1) Xét tam giác ABM và tam giác CDM có:
- AM = CM
- Góc AMB = góc CMD (2 góc đối đỉnh)
- BM = DM
-> Tam giác ABM = tam giác CDM (c.g.c)
2) Vì tam giác ABM = tam giác CDM
-> Góc MAB = góc MCD = 90o
-> MC vuông góc vs CD hay AC vuông góc vs DC
3) Vì E là trung điểm của BC , M là trung điểm của AC -> EM là đường trung trực của tam giác ABC -> EM//AB mà AB//DC (cùng vuông góc với AC) nên EM//DC hay MF//DC, ta có:
- M là trung điểm của AC (giả thiết)
- MF//DC (cmt)
Nên MF là đường trung trực của tam giác ACD
-> F là trung điểm của AD

a) Xét ΔABM và ΔCDM có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔABM=ΔCDM(c-g-c)
b) Ta có: ΔABM=ΔCDM(cmt)
nên \(\widehat{MAB}=\widehat{MCD}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(gt)
nên \(\widehat{MCD}=90^0\)
\(\Leftrightarrow\widehat{ACD}=90^0\)
hay AC\(\perp\)CD(Đpcm)

a/ \(\Delta ABM\)và \(\Delta CDM\)có:
BM = DM (gt)
\(\widehat{AMB}=\widehat{CMD}\)(đối đỉnh)
AM = CM (M là trung điểm AC)
=> \(\Delta ABM\)= \(\Delta CDM\)(c. g. c) (đpcm)
b/ Ta có \(\Delta ABM\)= \(\Delta CDM\)(cm câu a)
=> \(\widehat{ABM}=\widehat{CDM}\)(hai góc tương ứng) ở vị trí so le trong
=> AB // CD (đpcm)

a,Có BC^2=5^2=25
AB^2+AC^2=3^2+4^2=25
suy ra BC^2=AB^2+AC^2
Theo ĐL Pitago đảo thì tam giác ABC vuông tại A.