Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo nhé : ( Thứ tự các câu bị đảo lộn 1 xíu câu b) là câu c) còn câu c) là câu b) nhé ) :


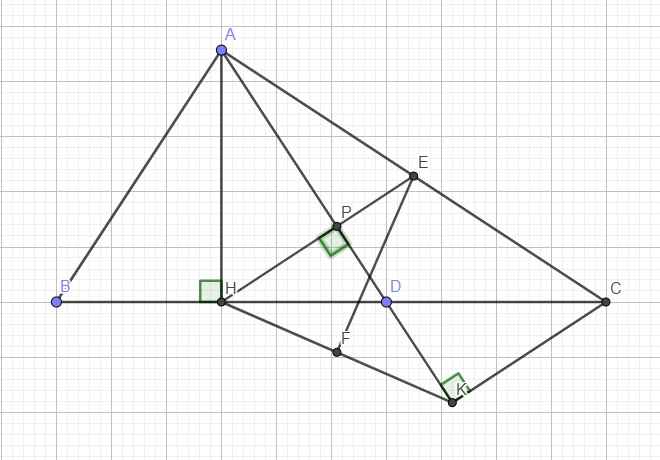
Gọi E là trung điểm AC, do H và K cùng nhìn AC dưới 1 góc vuông nên H, K thuộc đường tròn đường kính AC (1)
\(\Rightarrow EH=EK\) hay E nằm trên trung trực HK
Gọi F là trung điểm HK \(\Rightarrow F\left(2;-1\right)\)
\(\overrightarrow{HK}=\left(14;-8\right)=2\left(7;-4\right)\Rightarrow\) EF nhận (7;-4) là 1 vtpt
Phương trình EF: \(7\left(x-2\right)-4\left(y+1\right)=0\Leftrightarrow7x-4y-18=0\)
Tọa độ E là nghiệm: \(\left\{{}\begin{matrix}x-y+10=0\\7x-4y-18=0\end{matrix}\right.\) \(\Rightarrow E\left(\dfrac{58}{3};\dfrac{88}{3}\right)\)
\(\widehat{ACH}=\widehat{HAK}\) (cùng phụ \(\widehat{ABC}\)) \(\Rightarrow AH=HK\)
Mà \(AE=EK\) theo (1) \(\Rightarrow AK\) là trung trực EH
\(\overrightarrow{HE}=\left(\dfrac{73}{3};\dfrac{103}{3}\right)=\dfrac{1}{3}\left(73,103\right)\) \(\Rightarrow AK\) nhận \(\left(103;-73\right)\) là 1 vtpt
Tới đây bạn hãy kiểm tra lại số liệu, số liệu quá bất hợp lý
Tính tiếp như sau:
Viết pt AK (biết đi qua K và có vtpt như trên)
Tìm tọa độ giao điểm P của EH và AK
Khi đó P là trung điểm AK, tìm tọa độ A dễ dàng bằng công thức trung điểm

A B C I S D E F G K L K' M x
Gọi giao điểm khác D của hai đường tròn (BED);(CFD) là K'; K'I cắt EF tại L; DL cắt (I;ID) tại M khác D.
Ta thấy IE = IF; AI là phân giác ngoài của ^EAF, từ đây dễ suy ra 4 điểm A,E,I,F cùng thuộc một đường tròn
Vì 3 điểm D,F,E lần lượt thuộc các cạnh BC,CA,AB của \(\Delta\)ABC nên (BED);(CFD);(AFE) đồng quy (ĐL Miquel)
Hay điểm K' thuộc đường tròn (AIFE). Do vậy LI.LK' = LE.LF = LD.LM (= PL/(G) = PL/(I) )
Suy ra 4 điểm K',M,I,D cùng thuộc một đường tròn. Mà ID = IM nên ^IK'D = ^IK'M.
Đồng thời ^DIM = 1800 - ^DK'M = 1800 - ^EK'F + 2.^FK'D = ^BAC + 2.^ACB = 2.^AID
Suy ra IA vuông góc DM, từ đó M,L,D,A thẳng hàng (Vì IA cũng vuông góc AD)
Khi đó dễ thấy AL là phân giác ^BAC, K'L là phân giác ^EK'F, mà tứ giác AEK'F nội tiếp
Suy ra AEK'F là tứ giác điều hòa, từ đây AK' là đường đối trung của \(\Delta\)AEF
Suy ra K' trùng K. Kẻ tiếp tuyến Kx của (G), ta có ^BKx = ^EKx - ^EKB = ^EFK - ^EFD = ^BCK
Do đó (BKC) tiếp xúc với (G) tại K, tức KG đi qua tâm của (BKC) (1)
Gọi S là trung điểm cung lớn BC của (ABC). Có SB = SC và ^BKC = ^AED + ^AFD = 1800 - ^BSC/2
Suy ra S là tâm của đường tròn (BKC) (2)
Từ (1) và (2) suy ra KG luôn đi qua S cố định (Vì S là trung điểm cùng BC lớn cố định) (đpcm).

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.