Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để giải bài toán này, ta sẽ thực hiện theo từng phần như sau:
a. Tính AH
Trong tam giác vuông ABC, ta có:
- BH = 4 cm
- CH = 9 cm Áp dụng định lý Pytago-rơ: \(A B^{2} = B H^{2} + C H^{2}\) \(A B^{2} = 4^{2} + 9^{2} = 16 + 81 = 97\) \(A B = \sqrt{97} \approx 9.85 \&\text{nbsp};\text{cm}\) Vì tam giác ABC vuông tại A, nên AH là đường cao của tam giác. Áp dụng định lý Pytago-rơ: \(A H^{2} + H B^{2} = A B^{2}\) \(A H^{2} + 4^{2} = 97\) \(A H^{2} = 97 - 16 = 81\) \(A H = \sqrt{81} = 9 \&\text{nbsp};\text{cm}\)
b. Chứng minh tam giác ADE đồng dạng với tam giác ACB
Để chứng minh hai tam giác đồng dạng, ta cần chứng minh có ít nhất hai cặp cạnh tỷ lệ với nhau.
Xét tam giác ADE và tam giác ACB:
- Tam giác ADE và tam giác ACB đều là tam giác vuông.
- Góc A chung cho cả hai tam giác.
- Tỷ lệ AE/AC = AD/AB (vì AH là đường cao). Vậy hai tam giác ADE và ACB đồng dạng.
c. Kẻ đường thẳng vuông góc với DE tại E, cắt HC tại M. Tính sin DME
Theo định lý Pytago-rơ, ta có:
\(D M^{2} + M E^{2} = D E^{2}\)
Vì DE vuông góc với EM, nên:
\(s i n D M E = \frac{D M}{D E}\)

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC,ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=7,2\left(cm\right)\\BH=5,4\left(cm\right)\\CH=9,6\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HB\cdot HC=AE\cdot AB\)

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật

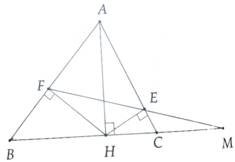
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
a: Ta có: BH+CH=BC
nên BC=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
hay AH=6(cm)