Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC

a: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
góc BAH chung
AB=AC
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: góc ABH+góc HBC=góc ABC
gócACK+góc ICB=góc ACB
mà góc ABC=góc ACB; góc ABH=góc ACK
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC

A B C O K H
a ) Vì \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)
Ta có : \(\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-\left(50^o+50^o\right)=180^o-100^o=80^o\)
b ) Xét \(\Delta KBC\) và \(\Delta HCB\) có :
\(\widehat{BKC}=\widehat{CHB}=90^o\)
BC là cạnh chung
\(\widehat{C}=\widehat{B}\left(cmt\right)\)
\(\Rightarrow\Delta KBC=\Delta HCB\) ( cạnh huyền - góc nhọn )
\(\Rightarrow KC=BH\)
C ) Vì \(\Delta KBC=\Delta HCB\left(cmt\right)\)
\(\Rightarrow\widehat{BCK}=\widehat{CBH}\)
\(\Rightarrow\Delta OBC\) cân tại O ( đpcm)

A B C O p/s:hình ảnh chỉ mang tc minh họa H K
a)Vì: ΔABC cân tại A(gt)
=> \(\widehat{B}=\widehat{C}=50^o\)
Có: \(\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-\left(50^o+50^o\right)=180^o-100^0=80^o\)
b)Xét ΔKBC và ΔHCB có:
\(\widehat{BKC}=\widehat{CHB}=90^o\)
BC: cạnh chung
\(\widehat{C}=\widehat{B}\left(cmt\right)\)
=> ΔKBC=ΔHCB(cạnh huyền-góc nhọn)
=>KC=BH
c)Vì: ΔKBC=ΔHCB(cmt)
=> \(\widehat{BCK}=\widehat{CBH}\)
=>ΔOBC cân tại O
Mk k vẽ hình nữa nha!!!
a/ Vì ΔABC cân tại A(gt) => \(\widehat{B}=\widehat{C}=50^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
hay \(\widehat{A}+50^o+50^o=180^o\Rightarrow\widehat{A}=180^o-50^o-50^o=80^o\)
b/ Xét 2 Δ vuông: ΔBKC và ΔCHB có:
BC: Cạnh chung
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> ΔBKC = ΔCHB (cạnh huyền - góc nhọn)
=> BH = CK (2 cạnh tương ứng) (đpcm)
c/ Vì ΔBKC = ΔCHB (ý b)
=> \(\widehat{HBC}=\widehat{KCB}\) (2 góc tương ứng)
=> ΔOBC cân tại O (đpcm)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC



 hãy cho mk 1 L-I-K-E
hãy cho mk 1 L-I-K-E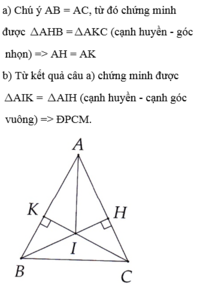
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K co
AB=AC
góc A chung
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAKH cân tại A