Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay MNCB là hình thang

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//BC
hay BEFC là hình thang

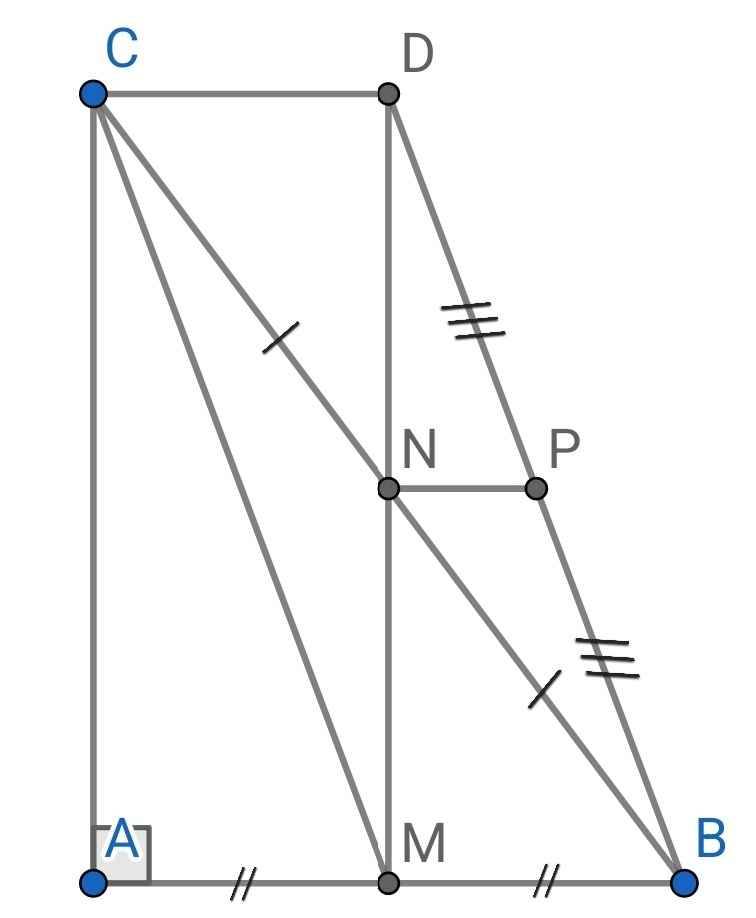 a) Do NM = ND (gt)
a) Do NM = ND (gt)
N ∈ MD
⇒ N là trung điểm của MD
Tứ giác BMCD có:
N là trung điểm của BC (gt)
N là trung điểm của MD (cmt)
⇒ BMCD là hình bình hành
b) Do M là trung điểm của AB (gt)
N là trung điểm của BC (gt)
⇒ MN // AC
⇒ MD // AC
Mà AC ⊥ AM (AB ⊥ AC)
⇒ MD ⊥ AM
⇒ ∠AMD = 90⁰
Do BMCD là hình bình hành (cmt)
⇒ CD // BM
⇒ CD // AM
Mà AM ⊥ AC (cmt)
⇒ CD ⊥ AC
⇒ ∠ACD = 90⁰
Tứ giác AMDC có:
∠CAM = ∠ACD = ∠AMD = 90⁰
⇒ AMDC là hình chữ nhật
c) ∆DMB có:
N là trung điểm của DM (cmt)
P là trung điểm của BD (gt)
⇒ NP // BM
⇒ NP // AB

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
\(\widehat{BAC}=90^0\)
Do đó: ABDC là hình chữ nhật
b: Xét ΔADE có
M,H lần lượt là trung điểm của AD,AE
=>MH là đường trung bình
=>MH//DE
=>DE vuông góc AE
Xét tứ giác ABED có \(\widehat{ABD}=\widehat{AED}=90^0\)
=>ABED là tứ giác nội tiếp
=>\(\widehat{BDE}=\widehat{EAB}\)
=>\(\widehat{BDE}=\widehat{HAB}=\widehat{C}\)
=>\(\widehat{BDE}=\widehat{C}\)
mà \(\widehat{ACB}=\widehat{ADB}\)
nên \(\widehat{BDE}=\widehat{ADB}\)
=>DB là phân giác của \(\widehat{ADE}\)

Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra:MN//BC
hay BMNC là hình thang
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay MNCB là hình thang