Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
b: Xét tứ giác NKIM có
D là trung điểm của NI
D là trung điểm của KM
Do đó: NKIM là hình bình hành
mà NI vuông góc với KM
nên NKIM là hình thoi
c: Xét ΔABC có DN//AB
nên DN/AB=CN/CA=CD/CB
=>CN=1/2CA
hay N là trung điểm của AC
Xét ΔABC có DM//AC
nên BM/BA=BD/BC=1/2
hay BM=1/2BA
=>M là trung điểm của AB
Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên MA=MH
Ta có: ΔAHC vuông tại H
mà HN là đừog trung tuyến
nên HN=AN
Xét ΔMAN và ΔMHN có
MA=MH
AN=HN
MN chung
Do đó: ΔMAN=ΔMHN
Suy ra:góc MHN=90 độ

Tứ giác AMIN có 3 góc vuông nên là HCH Tứ giác AICD có 2 đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành mà hình bình hành có 2 đường chéo vuông Nên tứ giác AICD là hình thoi (dhnb)

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a)Xét tứ giác AMDN có: góc AMD=900
góc MAN=900
góc DNA=900
=> Tứ giác AMDN là hình chữ nhật(dhnb hcn)
b)Xét tam giác ABC vuông tại A có:D là trung điểm của BC
=>AD là đường trung tuyến ứng với cạnh huyền BC
=>AD=BD=CD=BC/2
=> tg ACD cân tại D
Xét tg ACD cân tại D có: DN là đường cao
=>DN là đường trung tuyến của tam giác ADC
=>N là trung điểm của AC

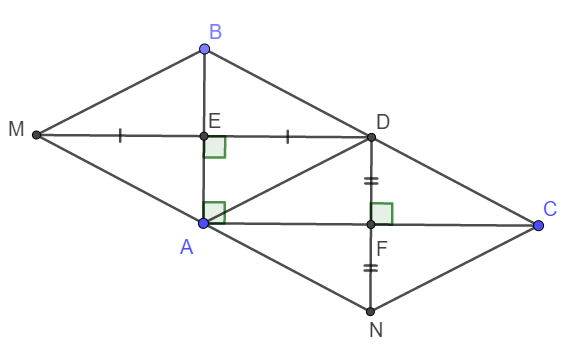
a) Tứ giác AEDF có 3 góc vuông nên AEDF là hình chữ nhật.
b) Do D là trung điểm BC nên E, F lần lượt là trung điểm của AB và AC.
Xét tứ giác ADBM có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Lại có \(AB\perp MD\) nên ADBM là hình thoi.
Tương tự ADCN cũng là hình thoi.
c) Ta có AB và AC lần lượt là phân giác của góc MAD và NAD
Vậy nên \(\widehat{MAN}=\widehat{MAD}+\widehat{NAD}=2\left(\widehat{BAD}+\widehat{FAD}\right)=180^o\)
Vậy M, A, N thẳng hàng.
Lại có AM = AD = AN nên A là trung điểm MN.
Hay M, N đối xứng nhau qua A.
d) Để hình chữ nhật AEDF trở thành hình vuông nên AE = AF hay AB = AC.
Vậy để AEDF là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A.
a) Tứ giác AEDF là hình chữ nhật
b) Tam giác ABC có BD = DC
DE//AC nên AE = BE
ta có DE =EM ( D đối xứng với M qua AB)Tứ giác ADBM có hai đường chéo cắt nhau tại trung điểm của mỗi dđường nện tứ giác ADBM là hình bình hành.
Tứ giác ADBM là hinh bình hành có hai đường chéo vuông góc AB vuông góc DM nên tứ giác ADBM là hình thoi

a: Xét tứ giác ANDM có
\(\widehat{AND}=\widehat{AMD}=\widehat{MAN}=90^0\)
=>ANDM là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của CB
DN//AB
Do đó: N là trung điểm của AC
Xét tứ giác ADCEcó
N là trung điểm chung của AC và DE
=>ADCE là hình bình hành
Hình bình hành ADCE có AC\(\perp\)DE
nên ADCE là hình thoi
c:
Xét ΔABC có
D là trung điểm của BC
DM//AC
Do đó: M là trung điểm của AB
Để AMDN là hình vuông thì AM=AN
mà \(AM=\dfrac{AB}{2};AN=\dfrac{AC}{2}\)
nên AB=AC
a) Ta có: MD vuông góc với ab
dn vuông góc với ac
nên: góc dma và góc dna =90 độ
và góc bac = 90 vì tam giác abc vuông tại a
vậy tứ giác là hcn (tg có 3 góc vuông)
b) đầu tiên bạn chứng minh DN là đường trung bình của tam giác abc suy ra DN // BA
Sau đó bạn c/m hbh có 2 đg chéo cắt nhau tại trung điểm của mỗi đường
mà BA vuông góc AC => DN vuông góc AC
Mà n là trung điểm DI (......)
SUY RA: DN vuông góc với AC
Vậy hbh ADCI là hình thoi (hbh có 2 đg chéo vuông góc với nhau)