Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì góc A = 90o , AD là tia phân giác góc A nên góc BAD = góc DAC = 90/2 = 45o.
Vì AH vuông góc với BC nên góc AHC=900
Trong tam giác HAC có : (góc) HAC + HCA + AHC = 180o
===> góc HAC + 400+900 = 1800
===> góc HAC = 500
Vì góc HAC > góc DAC (900>450) nên tia AD nằm giữa hai tia AC và AH
===> góc HAD + góc DAC = góc HAC
====> góc HAD + 450=500
===> góc HAD = 50

Ta có hình vẽ:
C D A H C B 40 a a'
Kẻ đường thẳng aa' đi qua điểm A sao cho aa' // BC
Vì AD là tia phân giác của CAB
=> \(CAD=DAB=\frac{CAB}{2}=\frac{90^o}{2}=45^o\)
Ta có: ACB = CAa' = 40o (so le trong)
Mà CAa' + CAD = DAa'
=> 40o + 45o = DAa'
=> DAa' = 85o
Do AH vuông góc với BC; aa' // BC => AH vuông góc với aa'
=> HAa' = 90o
Lại có: DAa' + HAD = HAa'
=> 85o + HAD = 90o
=> HAD = 90o - 85o
=> HAD = 5o

Vì góc A = 90o , AD là tia phân giác góc A nên góc BAD = góc DAC = 90/2 = 45o.
Vì AH vuông góc với BC nên góc AHC=900
Trong tam giác HAC có : (góc) HAC + HCA + AHC = 180o
===> góc HAC + 400+900 = 1800
===> góc HAC = 500
Vì góc HAC > góc DAC (900>450) nên tia AD nằm giữa hai tia AC và AH
===> góc HAD + góc DAC = góc HAC
====> góc HAD + 450=500
===> góc HAD = 50

a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)

a: 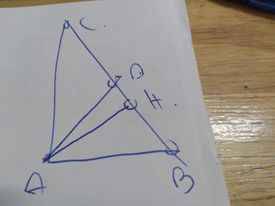
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot90^0=45^0\)
Xét ΔADC có \(\widehat{ADH}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADH}=\widehat{DAC}+\widehat{DCA}\)
=>\(\widehat{ADH}=45^0+30^0=75^0\)
b: ΔHAD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}+75^0=90^0\)
=>\(\widehat{HAD}=15^0\)
Vì \(\widehat{DAH}< \widehat{DAB}\)
nên AH nằm giữa AD và AB
=>\(\widehat{DAH}+\widehat{BAH}=\widehat{BAD}\)
=>\(\widehat{BAH}+15^0=45^0\)
=>\(\widehat{BAH}=30^0>\widehat{HAD}\)
d: \(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔAHC vuông tại H)
Do đó: \(\widehat{ABC}=\widehat{HAC}\)
`a)`

`b)`
Có `Delta ABC` vuông tại `A` có `hat(C)=30^0`
`=>hat(B)=60^0`
`AD` là phân giác `hat(BAC)=>hat(BAD)=hat(A_3)=1/2hat(BAC)`
`=>hat(BAD)=hat(A_3)=1/2*90^0=45^0`
`Delta BAD` có `hat(B)+hat(D_1)+hat(BAD)=180^0`
hay `60^0+hat(D_1)+45^0=180^0`
`=>hat(D_1)=180^0-60^0-45^0=75^0`
`c)`
Có `Delta AHD` vuông tại `H(AH⊥BC)` có `hat(D_1)=75^0`
`=>hat(A_1)=15^0`
Có `hat(A_1)+hat(A_2)=hat(BAD)`
hay`15^0+hat(A_2)=45^0`
`=>hat(A_2)=30^0`
Có `15^0<30^0`
`=>hat(A_1)<hat(A_2)`
`d)`
Có `hat(A_1)+hat(A_3)=hat(HAC)`
hay `15^0+45^0=hat(HAC)`
`=>hat(HAC)=60^0`
Có `60^0=60^0`
`=>hat(B)=hat(HAC)`

Tam giác ABC vuông tại A
=>góc BAC=90°
AD là tia phân giác của tam giác ABC
=>góc BAD=góc CAD=góc BAC/2=45°
Ta lại có,tam giác CAH vuông tại H( vì AH_|_BC theo gt)
=> góc AHC=90°
Xét tam giác vuông ACH,có:
góc HAC =180°-(góc AHC+góc ACH)
=180°-(90°+40°)=50°
=>góc HAD=góc HAC-góc DAC
=50°-45°
=5°
Ta có
tam giác AHC có
HAC+ AHC+HCA=180 nên HAC=180-AHC-HCA=180-90-40=50
Tam giác DAC có BAD=DAC=45( AD là tia phân giác)
Mà HAD+DAC=HAC nên HAD=5