Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của BC
D là trung điểm của AB
Do đó: MD là đường trung bình
=>MD//AC và MD=AC/2
hay MK=AC và MK//AC
Xét tứ giác ADMC có MD//AC
nên ADMC là hình thang
mà \(\widehat{CAD}=90^0\)
nên ADMC là hình thang vuông
b: Xét tứ giác KMCA có
KM//AC
KM=AC
Do đó: KMCA là hình bình hành

A B C D M N K
a) Vì: ^NAM=90 độ ( t/g ABC vuông tại A)
^AND=90 độ ( DN _|_ AB tại N
^AMD=90 độ (DM_|_ AC tại N)
=> AMDN là hcn ( tứ giác có 3 góc _|_ là hcn)
b) Ta có DN _|_ AB tại N
Mà K đối xứng với D qua N=>DN=KN=1/2KD
=> KD_|_ AB tại N (1)
Vì ANDM là hcn => ^AND=90 độ
=> AN_|_ND=>AN_|_KD (2)
Từ (1) và (2)=> ADBK là hình thoi ( theo t/chất hai đường chéo _|_)

a: Xét ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét tứ giác AMBE có
D là trung điểm chung của AB và ME
=>AMBE là hình bình hành
Hình bình hành AMBE có MA=MB
nên AMBE là hình thoi
=>AE//MB và AE=MB
AE//MB
M\(\in\)BC
Do đó: AE//MC
AE=MB
MB=MC
Do đó: AE=MC
Xét tứ giác ACME có
AE//MC
AE=MC
Do đó: ACME là hình bình hành
b: Hình thoi AEBM trở thành hình vuông khi \(\widehat{MBE}=90^0\)
=>\(\widehat{MBA}=\dfrac{90^0}{2}=45^0\)
=>\(\widehat{ABC}=45^0\)

Câu hỏi của nguuen thi minh tam - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Bạn tự vẽ hình nha!
a, Tứ giác AEDF là hình chữ nhật vì có 3 góc vuông (A=E=F=90 độ)
b, Ta có: D là TĐ của BC, DE vuông góc với AB
nên E là TĐ của AB .
Tứ giác ADBM có hai đường chéo AB,DM vuông góc với nhau tạ trung điểm của mỗi đường nên là hình thoi
Tương tự : ADCN là hình thoi (Bạn tự chứng minh nha!)

https://coccoc.com/search?query=cho+tam+gi%C3%A1c+abc+vu%C3%B4ng+t%E1%BA%A1i+a+am+l%C3%A0+trung+tuy%E1%BA%BFn
#Theo link này nhoooo

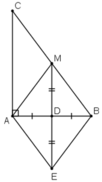
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.