Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
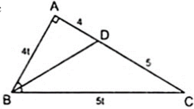
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
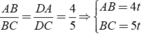với t > 0
Áp dụng định lý Py – ta – go ta có:
Khi đó: AB = 12cm, BC = 15cm
Lời giải:
Áp dụng tính chất tia phân giác:
$\frac{AD}{DC}=\frac{AB}{BC}$
$\Leftrightarrow \frac{3}{DC}=\frac{AB}{5}$
$\Rightarrow 15=AB.DC=AB(AC-AD)=AB(AC-3)(1)$
Mà: $AB^2+AC^2=BC^2=25(2)$
Từ $(1); (2)\Rightarrow (\frac{15}{AC-3})^2=AB^2=25-AC^2$
$\Leftrightarrow AC^4-6AC^3-16AC^2+150AC=0$
$\Leftrightarrow AC^3-6AC^2-16AC+150=0$
PT giải ra số khá xấu. Bạn xem lại đề.
A B C H D
Ta có AD là tia phân giác \(\widehat{BAC}\)
=> \(\frac{BD}{DC}=\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}\)
mà BD + DC = BC = 35
Lại có AB2 + AC2 = BC2 (định lý pi-ta-go trong tam giác vuông ABC)
<=> \(\left(\frac{3}{4}AC\right)^2+AC^2=35^2\)
<=> \(AC^2.\frac{25}{16}=35^2\)
<=> AC = 28
=> AB = 21
Xét tam giác HAC và tam giác ABC có :
\(\hept{\begin{cases}\widehat{C}\text{ chung}\\\widehat{CAB}=\widehat{CHA}\end{cases}}\Leftrightarrow\Delta ABC\approx\Delta HAC\left(g-g\right)\)(1)
Tương tự \(\Delta ABC\approx HBA\)(g-g) (2)
Từ (1) và (2) => \(\Delta HAC\approx\Delta HBA\)
=> \(\frac{AB}{AC}=\frac{AH}{CH}=\frac{HB}{HA}=\frac{3}{4}\)
mà AH2 + CH2 = AC2 (ĐỊNH LÝ PITAGO)
=>\(\left(\frac{3}{4}CH\right)^2+CH^2=21^2\)
<=> \(\frac{25}{16}CH^2=21^2\)
<=> CH = 16,8 cm
=> BH = BC - CH = 35 - 16,8 = 18,2
=> DH = BH - BD = 18,2 - 15 = 3,2
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔBAC có BD là phan giác
=>AD/AB=DC/BC
=>AD/3=DC/5=8/8=1
=>AD=3cm; DC=5cm
b: Xét ΔBAD vuông tại A va ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>AD/HI=BA/BH
=>AD*BH=HI*BA
c: góc ADI=góc BIH=góc AID
=>ΔAID cân tại A
Áp dụng tính chất đường phân giác BD của tam giác
ABC, ta có:
Áp dụng định lý Py – ta – go ta có:
B C 2 = A C 2 + A B 2 hay ( 5 t ) 2 = 9 2 + ( 4 t ) 2 ⇔ ( 3 t ) 2 = 9 2 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm