Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

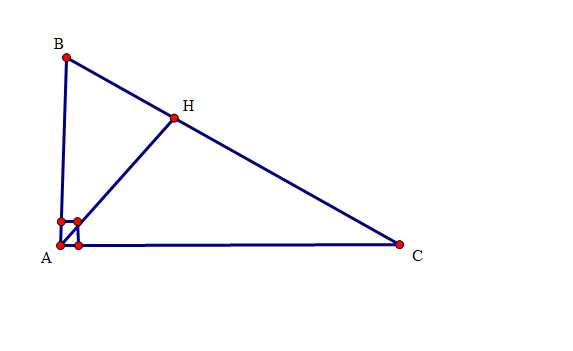
a, \(\Delta ABC\)và \(\Delta HBA\)có:
\(\widehat{ABC}=\widehat{AHB}=90^o\)
\(\widehat{BAC}\) chung
\(\Rightarrow \Delta ABC \sim \Delta HBA\) (g-g)
b, Ta có: \(\Delta ABC \sim \Delta HBA\) (g-g) \(\Rightarrow\frac{AC}{AH}=\frac{BC}{AB}\)\(\Rightarrow AB.AC=AH.BC\)
c, \(\Delta ABC\)có: \(\widehat{BAC}=90^o\)
\(\Rightarrow BC^2=AB^2+AC^2\)(định lý Py-ta-go)
hay \(10^2=6^2+AC^2\)
\(AC^2=64\)
\(AC=8\left(cm\right)\)
Ta có: \(\frac{AC}{AH}=\frac{BC}{AB}\left(cmt\right)\Leftrightarrow\frac{8}{AH}=\frac{10}{6}\Leftrightarrow AH=4,8\left(cm\right)\)
\(\Delta AHC\)có: \(\widehat{AHC}=90^o\)
\(\Rightarrow AC^2=AH^2+HC^2\)(định lý Py-ta-go)
hay \(8^2=4,8^2+HC^2\)
\(HC^2=40,96\)
\(HC=6,4\left(cm\right)\)

a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
bn ơi câu a bn giải thích ra luôn giùm mik ik
câu b,c nx

a) xét tam giác ABH và tam giác CBA
có góc B chung
góc AGB= góc BAC=90
=>tam giác ABH đồng dạng tam giác CBA
=>\(\dfrac{AB}{CB}=\dfrac{AH}{CA}\)
b) áp dụng định lý pytago có
AB2+AC2=BC2
Thay AB=8;AC=6
=>BC=10
Theo câu a)có:\(\dfrac{AB}{CB}=\dfrac{AH}{CA}\)
thay số \(\dfrac{8}{10}=\dfrac{AH}{6}\)
=>AH=4,8

A B C H 6 8
a, Xét tam giác HBA và tam giác ABC ta có :
^AHB = ^BAC = 900
^B _ chung
Vậy tam giác HBA ~ tam giác ABC ( g.g )
b, Xét tam giác ABC vuông tại A, AH là đường cao
Áp dụng định lí Pytago cho tam giác ABC :
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Vì tam giác HBA ~ tam giác ABC ( cma )
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow\frac{AH}{8}=\frac{6}{10}\Rightarrow AH=\frac{48}{10}=\frac{24}{5}\)cm

a: Đề sai rồi bạn
b: BC=căn 8^2+6^2=10cm
S ABC=1/2*AB*AC=24cm2
Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
=>BA/BC=BH/BA=6/10=3/5 và S BAH/S BCA=(3/5)^2=9/25
=>DH/DA=3/5
=>HD/HA=3/8
=>S BHD=3/8*S HBA=3/8*9/25*S BCA=27/200*S BCA
Vì tam giác ABC vuông tại A nên ta có
BC2=AB2+AC2
= >AC2=BC2-AB2
TỰ LÀM TIẾP