Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pytago ra BC=35
Áp dụng hệ thức lượng ra:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{441}+\frac{1}{784}\Rightarrow AH=\frac{84}{5}\)
AB2=HB.BC→HB=441:35=12.6
HC=BC-HB=35-12.6=22.4
b, Tính theo ct thôi vì biết các cạnh rồi.
c,Theo t/c đường phân giác có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{BD}{CD}=\frac{3}{4}\Rightarrow\frac{BD+CD}{CD}=\frac{3+4}{4}\Rightarrow\frac{BC}{CD}=\frac{7}{4}\Rightarrow CD=20;BD=15\)

a) Áp dụng HTL :
\(\left\{{}\begin{matrix}AH^2=BH.HC\Rightarrow AH=\sqrt{1,8.3,2}=2,4\left(cm\right)\\AB^2=BH.BC\Rightarrow AB=\sqrt{1,8\left(1,8+3,2\right)}=3\left(cm\right)\\AC^2=HC.BC\Rightarrow AC=\sqrt{3,2\left(1,8+3,2\right)}=4\left(cm\right)\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}tanB=\dfrac{AC}{AB}=\dfrac{4}{3}\Rightarrow\widehat{B}\approx53^0\\tanC=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow\widehat{C}\approx37^0\end{matrix}\right.\)
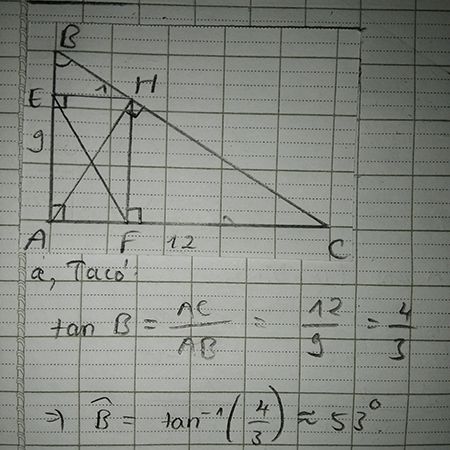


a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
hay BC=15(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{9}=\dfrac{CD}{12}\)
mà BD+CD=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\dfrac{BD}{9}=\dfrac{CD}{12}=\dfrac{15}{21}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{45}{7}cm;CD=\dfrac{60}{7}cm\)