Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

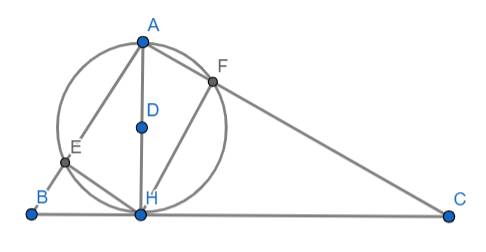
1) Ta có: \(\Delta AHF\) nội tiếp đường tròn (D) có AH là đường kính
\(\Rightarrow\widehat{AFH}=90^o\) (1)
\(\Delta AHE\) nội tiếp đường tròn (D) có AH là đường kính
\(\Rightarrow\widehat{AEH}=90^o\) (2)
Mà: \(\widehat{EAF}=90^o\left(gt\right)\) (3)
Từ (1), (2), (3) \(\Rightarrow\) Tứ giác AEHF có 3 góc vuông nên là hình chữ nhật
2) Áp dụng hệ thức lượng cho ΔABH có đường cao HE ta có:
\(AE\cdot AB=AH^2\) (4)
Áp dụng hệ thức lượng cho ΔACH có đường cao HF ta có:
\(AF\cdot AC=AH^2\) (5)
Từ (4) và (5) ta có: \(AE\cdot AB=AF\cdot AC\left(đpcm\right)\)

a) Xét (O) có
ΔAFH nội tiếp đường tròn(A,F,H\(\in\)(O))
AH là đường kính(gt)
Do đó: ΔAFH vuông tại F(Định lí)
Xét (O) có
ΔAEH nội tiếp đường tròn(A,E,H\(\in\)(O))
Do đó: ΔAEH vuông tại E(Định lí)
Xét tứ giác AEHF có
\(\widehat{FAE}=90^0\left(\widehat{BAC}=90^0\right)\)
\(\widehat{AEH}=90^0\)(ΔAEH vuông tại E)
\(\widehat{AFH}=90^0\)(ΔAHF vuông tại F)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

a) ta có : O là trung điểm của AH
xét đường tròn tâm O,có:E thuộc đường tròn
→tam giác A,E,H vuông tại E (t/c đường tròn)
F thược đường tròn
→tam giác A,F,H vuông tại F (t/c đường tròn)
Xét tứ giác A,E,H,F ta có Â =90 (ΔA,B,C vuông tại A)
Ê = F =90 (Δ vuông )
→tứ giác A,E,H,F là hình chữ nhật

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

a: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2=AE*AB
=>AE/AC=AF/AB
=>ΔAEF đồng dạng vơi ΔACB