
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

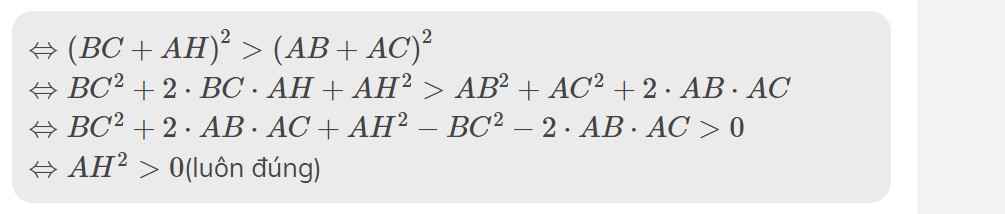

\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)

Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).



Ta có: góc ABC = góc BAC + góc ACB (Tam giác abc vuông tại a)
=> BC = AB + AC (Quan hệ giữa góc và cạnh đối diện)
=> BC + AH > AB + AC
Hay AB + AC < BC + AH

\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{AB\cdot AC}{2}\)
Do đó: \(AH\cdot BC=AB\cdot AC\)