Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
B A C D H H
a,Xét ΔBAH và ΔBCA,có:
\(\widehat{B}\) : góc chung
\(\widehat{BHA}=\widehat{BAC}=90^0\)
⇒ ΔBAH ∼ ΔBCA (1) (gg)
⇒ \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
⇒ \(AB^2=BH.BC\)
C/m tương tự:
\(\Delta ACH\sim\Delta BCA\left(gg\right)\left(2\right)\)
\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CH}{AC}\Rightarrow AC^2=CH.BC\)
Từ(1)(2) ⇒ ΔBAH ∼ ΔACH
⇒ \(\dfrac{BH}{AH}=\dfrac{AH}{CH}\Rightarrow AH^2=BH.CH\)
b,Vì AD là phân giác của ΔBAC
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{DB}{DC}=\dfrac{1}{2}\)
ΔBAH ∼ ΔACH
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BH}{AH}=\dfrac{AH}{CH}\)
hay \(\dfrac{1}{2}=\dfrac{BH}{AH}=\dfrac{AH}{CH}\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{1}{2}AH\\CH=2AH\end{matrix}\right.\Rightarrow\dfrac{HB}{HC}=\dfrac{\dfrac{1}{2}AH}{2AH}=\dfrac{1}{4}\)

a) Ta thấy: \(AB.AC=BC.AH\)
\(\Leftrightarrow AB^2.AC^2=BC^2.AH^2\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{BC^2}\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{AB^2+AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{AB^2+AC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
Ta có: \(\frac{AB}{AC}=\frac{5}{7}\Rightarrow AB:AC=\frac{5}{7}\Rightarrow AB=\frac{5}{7}AC\)
Áp dụng công thức trên: \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{15^2}=\frac{1}{\frac{25}{49}AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{49}{25}.\frac{1}{AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{1}{AC^2}\left(\frac{49}{25}+1\right)\)
\(\Rightarrow\frac{1}{225}=\frac{1}{AC^2}.\frac{74}{25}\Rightarrow\frac{1}{AC^2}=\frac{1}{225}.\frac{25}{74}=\frac{1}{666}\Rightarrow AC^2=666\Rightarrow AC=\sqrt{666}=3\sqrt{74}cm\)
Do đó: \(AB=\frac{5}{7}.3\sqrt{74}=\frac{15\sqrt{74}}{7}cm\)
Xét tam giác ABH có: \(AH^2+BH^2=AB^2\Leftrightarrow15^2+BH^2=\left(\frac{15\sqrt{74}}{7}\right)^2\Leftrightarrow BH^2=\frac{16650}{49}-225=\frac{5625}{49}\)
\(\Rightarrow BH=\frac{\sqrt{5625}}{\sqrt{49}}=\frac{75}{7}cm\)
Xét tam giác ACH có: \(AH^2+HC^2=AC^2\Leftrightarrow15^2+HC^2=666\Leftrightarrow HC^2=666-225=441\)
\(\Rightarrow HC=\sqrt{441}=21cm\)
Vậy: \(BH=\frac{75}{7}cm\) và \(HC=21cm\)
b) Chu vi tam giác ABC là: \(AB+AC+BC=\frac{15\sqrt{74}}{7}+3\sqrt{74}+21+\frac{75}{7}\approx76cm\)
A B C H 15 cm
Vì tam giác ABC vuông tại A => góc B + góc C = 90o
Vì tam giác HAC vuông tại H => góc HAC + góc C = 90o
=> góc HAC = góc B
Xét tam giác HAC và tam giác HBA có:
góc HAC = góc B (cmt)
góc AHC = góc AHB (=90o)
=> tam giác HAC đồng dạng với tam giác HBA (TH3)
=> \(\frac{AC}{AB}=\frac{AH}{BH}=\frac{HC}{AH}=\frac{7}{5}\)
=> \(HC=15.\frac{7}{5}=21\left(cm\right);HB=15.\frac{5}{7}=\frac{75}{7}\left(cm\right)\)
Sau đó tính AB; AC; BC. Ngại là lắm, làm nốt nhá ._.

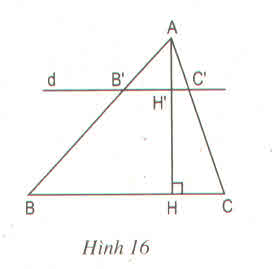
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

lỗi
CK là phân giác ΔABC =>KB/KA=BC/AC
CK là phân giác ΔAHC =>MH/MA=HC/AC
CK là phân giác \(\Delta_{ABC}\) =>\(\dfrac{KB}{KA}=\dfrac{BC}{AC}\) (1)
CK là phân giác \(\Delta_{AHC}\) =>\(\dfrac{MH}{MA}=\dfrac{HC}{AC}\) (2)


(AB/AC)^2=HB/HC
=>(AB/AC)^2=9/16
=>AB/AC=3/4