Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)

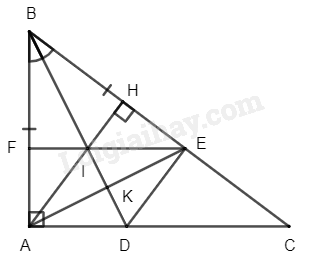
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(BA = BE\) (gt)
\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)
\(BD\) chung
Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD = \Delta EBD\) (cmt)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\)
Mà \(AH \bot BC\) (gt)
Suy ra \(AH\) // \(DE\)
Suy ra \(ADEH\) là hình thang
Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)
Suy ra \(ADEH\) là hình thang vuông
c)
Gọi \(K\) là giao điểm của \(AE\) và \(AD\)
Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)
Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )
Suy ra \(BK\) cũng là đường cao
Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)
Suy ra \(I\) là trực tâm của \(\Delta ABE\)
Suy ra \(EF \bot AB\)
Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))
Suy ra \(AC\) // \(EF\)
Suy ra \(ACEF\) là hình thang
Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)
Suy ra \(ACEF\) là hình thang vuông

A B C E F H I
Giải
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (vì đối đỉnh)
\(\widehat{BFH}=\widehat{CEH}=90^o\)
=> \(\Delta BHF\) s \(\Delta CHE\) (g - g)
b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{A}\) là góc chung
\(\widehat{AEB}=\widehat{AFC}=90^o\)
=> \(\Delta ABE\) s \(\Delta ACF\) (g - g)
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
=> AF . AB = AE . AC
c) Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{A}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\) (vì \(\Delta ABE\) s \(\Delta ACF\))
=> \(\Delta AEF\)s \(\Delta ABC\) (c - g - c)
d) Câu d mình không nghĩ ra. Bạn tự làm nha, chắc là xét tam giác đồng dạng rồi suy ra hai góc bằng nhau và sẽ suy ra đường phân giác đó.

Lời giải:
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
Ta có:
$AB.AC=AH.BC$ (cùng bằng 2 lần diện tích tam giác $ABC$)
b.
Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ góc $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$
$\Rightarrow AH^2=BH.CH$.

1) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Suy ra: \(\dfrac{HB}{AB}=\dfrac{AB}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)
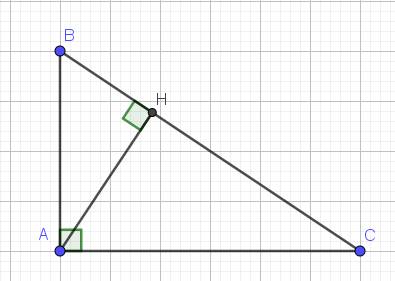
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
b: Xét ΔABD và ΔCBE có
\(\widehat{ABD}=\widehat{CBE}\)(BE là phân giác của góc ABC)
\(\widehat{BAD}=\widehat{BCE}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔABD~ΔCBE