Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

t nghĩ câu a, bạn làm được rồi
b) thì bn chứng minh \(\Delta HDA\infty HCB\left(c-g-c\right)\)
=> ĐPCM
c) thì bạn kẻ HE cắt BC tại M
Thì bn dùng đồng dạng chứng minh được \(BE.BA=BM.BC;CE.CD=CM.CB\)
rồi cộng vào sẽ = BC^2 k đổi
^^

Bài này mk làm rồi nha
Bạn tham khảo ở link :
https://olm.vn/hoi-dap/question/1177459.html
Bài này mình mới giải cho bạn huytran
Bạn tham khảo ở linh sau :
htpps://olm.vn/hoi-dap/question/1177459.html

a: Xet tứ giác ADBC có
góc CDB=góc CAB=90 độ
=>ADBC là tứ giác nội tiếp
b: Xét tứ giác AEDH có
góc EAH+góc EDH=180 độ
=>AEDH là tứ giác nội tiếp
=>góc ADH=góc AEH


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 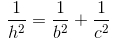
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

a, Ta có : góc BDC = góc BAC = 90 độ
=> tứ giác BDAC nội tiếp
b, Tứ giác ADBC nội tiếp
BD cắt AC ở H
=> góc HDA = góc ACB ko đổi
c, Có : BA.BE + CD.CE
= (BE+EA).BE + (CE+ED).CE
= BE^2 + CE^2 + EA.BE + ED.CE
= BE^2 + EA^2 + AC^2 + EA.BE + ED.CE
Tứ giác ADBC nội tiếp => góc BAD = góc BCD
=> tam giác DEA đồng dạng với tam giác BEC (g.g)
=> DE/BE = EA/EC
=> DE.EC = EA.EB
=> BE.BA + CE.CD = BE^2 + AE^2 + AC^2 + 2.EA.EB
= (BE+AE)^2 + AC^2 = AB^2 +AC^2 ko đổi
Tk mk nha