Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

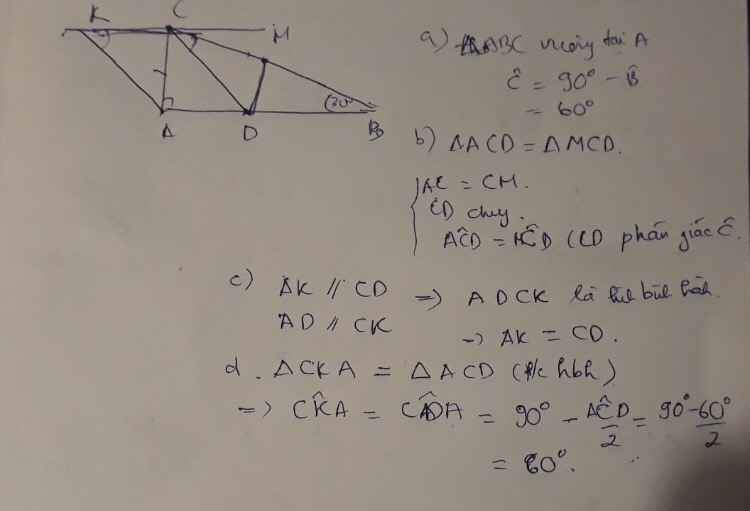
a, Xét ∆ABC vuông tại A có: B + C = 90o
=> 30o + C = 90o
=> C = 60o
b, Vì CD là tia phân giác của C
=> ACD = DCB = ACB/2 = 60o/2 = 30o
Xét ∆ACB và ∆MCD
Có: AD: cạnh chung (gt)
ACD = DCM (vì CD là tia p/g của C)
CA = CM (gt)
=> ∆ACB = ∆MCD (c.g.c)
c, XY vuông góc CA => KCA = 90o
Vì AK // CD => CKA = CDA (2 góc so le trong)
Xét ∆CAK vuông tại C và ∆ADC vuông tại A
Có: CA: cạnh chung
CKA = CDA (cmt)
=> ∆CAK = ∆ADC (cgv-gn)
=> AK = DC (2 cạnh tương ứng)
d, Vì ∆CAK = ∆ADC (câu c)
=> KAC = ACD (2 góc tương ứng)
Mà ACD = 30o
=> KAC = 30o
Xét ∆KAC vuông tại C có: KAC + AKC = 90o
=> 30o + AKC = 90o
=> AKC = 60o

a. Ta có A+B+C=180 độ ( tổng 3 góc trong tam giác)
=> C= 180 độ - ( A+B) =60 độ
b. Xét 2 tam giác vuông : tam giác : DCA và DCM có :
DC chung; góc DCA = góc DCM ( cd là phân giác của acm ); CM=CA (gt)
=>tam giác DCM=tam giác DCA (c.g.c)
c. xét hai tam giác vuông : DCA và KAC có :
AC chung; góc DCA = góc CAK ( so le trong vì DC // AK )
=> DCA=KAC(cgv. gn )=>AK=CD(2 góc tương ứng )
d. ta có: tam giác : DCA = KAC ( câu c)=>AKC=ADC (2 góc tương ứng)
Mà CAK+AKC+KCA=180 độ ( tổng 3 góc trong tam giác)
=>AKC= 180-90-30=60 độ
vì KAC=ACD60/2=30 độ

mk viết ngắn gọn thui nhé:
a) góc C = 1800 - Â - B = 1800 - 900 - 300 = 600
b) * tam giác ACD = tam giác MCD (c.g.c) . Vì:
CD : cạnh chung
góc ACD = góc MCD
AC = MC
* Xét 2 tam giác vuông: ACK và CDA:
góc ACD = góc CAK (2 góc so le trong)
AC : cạnh chung
=> tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)
=> AK = CD (2 cạnh tương ứng)
c) theo câu b: tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)
=> góc AKC = góc ADC (2 góc tương ứng)
Trong tam giác ACD, có:
góc ADC = 1800 - góc A - (góc ACB : 2) = 1800 - 900 - 600 : 2 = 600
=> góc AKC = góc ADC = 600

Bài 1: Ta có hình vẽ sau:
B A C M E
a)Xét ΔABM và ΔECM có:
BM = CM (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đỗi đỉnh)
MA = ME (gt)
=> ΔABM = ΔACM (c.g.c) (đpcm)
b) Vì ΔABM = ΔECM (ý a)
=> \(\widehat{MAB}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> AB // CE (đpcm)
Bài 5: Ta có hình vẽ sau:
O A B D C x y E
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
\(\widehat{O}\) : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> \(\widehat{OBC}=\widehat{OAD}\) và \(\widehat{ODA}=\widehat{OCB}\)
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
\(\widehat{OBC}=\widehat{OAD}\) (cm trên)
AC = BD (gt)
\(\widehat{ODA}=\widehat{OCB}\) (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
\(\widehat{OBC}=\widehat{OAD}\) (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
=> OE là phân giác của \(\widehat{xOy}\)