Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bn tự vẽ hình nha
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn)
Tớ chỉ lm đc câu a thui nếu đúng like cho tớ nha![]()

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
=>AM=HK
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
M,K lần lượt là trung điểm của CB,CA
=>MK là đường trung bình của ΔABC
=>MK//AB và \(MK=\dfrac{AB}{2}\)
Ta có: MK//AB
H\(\in\)AB
Do đó: MK//HB
Ta có: \(MK=\dfrac{AB}{2}\)
\(AH=HB=\dfrac{AB}{2}\)
Do đó: MK=AH=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
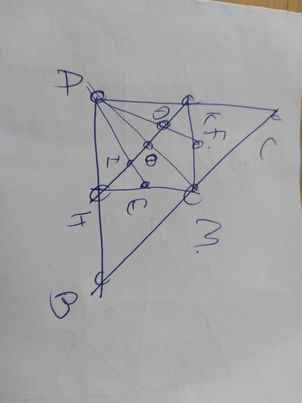
c: Gọi O là giao điểm của AM và KH
Ta có: AHMK là hình chữ nhật
=>AM cắt KH tại trung điểm của mỗi đường
=>O là trung điểm của AM và KH
=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)
mà AM=KH
nên OA=OM=OK=OH(1)
Xét ΔAKM có
AF,KO là các đường trung tuyến
AF cắt KO tại D
Do đó: D là trọng tâm của ΔAKM
Xét ΔAKM có
D là trọng tâm
KO là đường trung tuyến
Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)
Xét ΔHAM có
AE,HO là các đường trung tuyến
AE cắt HO tại I
Do đó: I là trọng tâm của ΔHAM
Xét ΔHAM có
HO là đường trung tuyến
I là trọng tâm
Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)
Từ (1),(2),(3) suy ra HI=KD

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

a: Xét tứ giác AKMH có
\(\widehat{AKM}=\widehat{AHM}=\widehat{KAH}=90^0\)
Do đó: AKMH là hình chữ nhật
b: Xét tứ giác BMKH có
MK//BH
MK=BH
Do đó: BMKH là hình bình hành
Suy ra: BK và MH cắt nhau tại trung điểm của mỗi đường
mà E là trung điểm của MH
nên E là trung điểm của BK
=>B,E,K thẳng hàng
thanks nha , kb vs mik nhek