HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AV
13 tháng 3 2019
A B C H
a) ta có SABC= 1/2.AB.AC=1/2AH.BC(L7cmroi)
b) △ABC~△BHA(gg)=> \(\frac{AB}{BH}=\frac{BC}{AB}\Leftrightarrow AB^2=BH.BC\left(đpcm\right)\)
c)△BHA~△AHC(g-g(cùng ~△ABC))=> \(\frac{AH}{BH}=\frac{CH}{AH}\Leftrightarrow AH^2=BH.CH\left(cmx\right)\)
13 tháng 3 2019
ta chứng minh được tam giác HCA ~tam giác ACB (g.g) do : ^CHA = ^CAB(=90 độ) và ^HCA=^ACB(do H thuộc BC) => AH :AB = AC : BC => AH. BC =AC.AB
b) tương tự ta c/m tam giác HBA ~ tam giác ABC (g.g) lí do tương tự như bên trên có hai góc =90 độ (xem trong hình vẽ ^BHA=^BAC) VÀ có chung 1 góc abc => AB:BC=BH:AB=>AB.AB=BH.BC
C) Có tam giác HCA ~ tam giác ACB => ^HAC=^ABC(2 góc tương ứng) mà có góc HCA+góc HAC =90độ(t/c trong tam giác vuông) mặt khác ta cũng có góc ABH + HAB = 90độ (do tam giác ABC vuông tại A) => GÓC HCA =góc HAB ( cùng phụ với góc HAC và ABH) CHÚ Ý góc ABH = góc ABC . CUỐI cùng c/m tam giác HCA ~ tam giác HAB (g.g) => ah :ch =bh : ah => AH .AH =BH .CH
6 tháng 6 2019
b, Xét \(\Delta ABHvà\Delta CBAcó:\)
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{ABH}=\widehat{CBA}\)(là góc chung)
Vậy \(\Delta ABH\sim\Delta CBA\left(g-g\right)\)
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\)
\(\Rightarrow AB.AB=BC.BH\)
\(\Rightarrow AB^2=BC.BH\left(đpcm\right)\)
6 tháng 6 2019
a,Xét \(\Delta BACvà\Delta AHCó:\)
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{BCA}=\widehat{ACH}\)(là góc chung)
Vậy \(\Delta BAC\sim\Delta AHC\left(g-g\right)\)
16 tháng 6 2022
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
Do đó: ΔABH\(\sim\)ΔCBA
Suy ra: BA/BC=BH/BA
hay \(BA^2=BH\cdot BC\)
Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
Do đo: ΔACH\(\sim\)ΔBCA
Suy ra: CA/CB=CH/CA
hay \(CA^2=CH\cdot CB\)
b: \(BC^2=AB^2+AC^2\)
c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔAHB\(\sim\)ΔCHA
Suy ra: HA/HC=HB/HA
hay \(HA^2=HB\cdot HC\)
1 tháng 5 2018
A B C H
a, Xét ΔABC và ΔHBA ,có :
\(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{B}:\) góc chung
⇒ ΔABC ∼ ΔHBA (gg) (1)
Xét ΔHAC và ΔABC,có :
\(\widehat{AHC}=\widehat{BAC}=90^0\)
\(\widehat{C}:\) góc chung
⇒ ΔHAC ∼ ΔABC (gg) (2)
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
\(\Rightarrow AB.AC=AH.BC\)
b, Từ (1)(2) ⇒ ΔHBA ∼ ΔHAC
\(\Rightarrow\dfrac{BH}{AH}=\dfrac{AH}{CH}\)
\(\Rightarrow AH.AH=BH.CH\)
hay \(AH^2=BH.CH\)
PT
1
CM
13 tháng 1 2017
S = A B C 1 2 A H . B C = 1 2 A B . A C
Þ AH.BC = AB.AC (ĐPCM)
14 tháng 1 2024
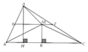
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
b: Xét ΔABD và ΔCBE có
\(\widehat{ABD}=\widehat{CBE}\)(BE là phân giác của góc ABC)
\(\widehat{BAD}=\widehat{BCE}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔABD~ΔCBE
VT
17 tháng 6 2018
A B C H M N
a)Ta có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
Vì ΔABC vuôgn tại A nên SABC = \(\dfrac{AB.AC}{2}\)
Do đó \(\dfrac{AB.BC}{2}=\dfrac{AH.BC}{2}\)
Vậy AB.AC = AH.AB
b) Xét ΔABC và ΔHBA, có:
\(\widehat{A}=\widehat{H}\left(90^o\right)\)
\(\widehat{B}:chung\)
Nên ΔABC ∼ ΔHBA (g.g)
=> \(\dfrac{AB}{BH}=\dfrac{BC}{AB}\) (tỉ số đồng dạng)
Vậy AB2 = BH.BC
c) Xét ΔABH và ΔCAH, có:
\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ \(\widehat{CAH}\) )
\(\widehat{ABH}=\widehat{CAH}\) (cùng phụ \(\widehat{BAH}\) )
Suy ra ΔABH ~ ΔCAH(g.g)
=> \(\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
Vậy (đpcm)
d) Xét ΔABH, có: AN = HN (gt) , BM = HM (gt)
⇒ MN là đường trung bình của ΔABH
⇒ MN // AB
Mà AB ⊥ AC
Nên MN ⊥ AC
Xét ΔACM, có:
AH ⊥ MC (gt), MN ⊥ AC (cmt)
\(AH\cap MN=\left\{N\right\}\)
Do đó N là trực tâm ΔACM
⇒ CN ⊥ AM (đpcm)
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Lời giải:
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
Ta có:
$AB.AC=AH.BC$ (cùng bằng 2 lần diện tích tam giác $ABC$)
b.
Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ góc $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$
$\Rightarrow AH^2=BH.CH$.
KK
25 tháng 2 2019
A B C H
Giải: a) Ta có : \(S_{\Delta ABC}\)= \(\frac{AH.BC}{2}\) (1)
\(S_{\Delta ABC}\)= \(\frac{AB.AC}{2}\) (2)
Từ (1) và (2) suy ra \(\frac{AH.BC}{2}=\frac{AB.AC}{2}\) => AH.BC = AB.AC (Đpcm)
b) Xét t/giác ABC vuông tại A (áp dụng định lí Pi - ta - go)
Ta có: BC2 = AB2 + AC2 = 152 + 202 = 225 + 400 = 625
=> BC = 25
Ta có: AH.BC = AB.AC (cmt)
hay AH. 25 = 15.20
=> AH.25 = 300
=> AH = 300 : 25
=> AH = 12
c) chưa hc
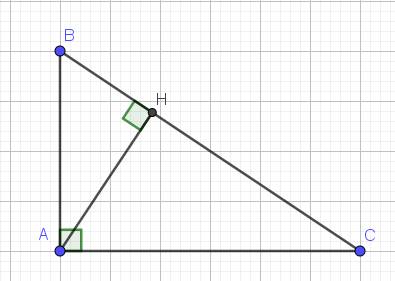
Áp dụng các hệ thức lượng trong tam giác vuông ,ta được:
\(AH^2=BH.CH\)
\(AH.BC=AB.AC\)
Lớp 8 chưa học lượng giác mà??
a) Xét tam giác AHC vuông tại H và tam giác AHB vuông tại H
Áp dụng định lý Pytago cho cả 2 tam giác:
Tam giác AHC: AH^2= AC^2 - CH^2 (1)
TAM GIÁC AHB: AH^2 =AB^2 - BH^2 (2)
(1) (2) Suy ra 2AH^2 = AB^2 + AC^2 - CH^2 - BH^2
2AH^2 = BC^2 - CH^2 - BH^2
2AH^2 = (BH+CH)^2 - CH^2 - BH^2
2AH^2 = 2BH.CH
AH^2 = BH.CH
b) Xét tam giác AHB và tam giác CAB:
H^ = A^ = 90 độ
B^ chung
2 tam giác AHB và tam giác CAB đồng dạng trường hợp (g-g)
Suy ra AH/CA = HB/AB= AB/BC
Vậy AH.BC = AB.AC