NK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 8 2020
A B C a 2a
Áp dụng định lí Pi-ta-go cho \(\Delta ABC\)vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=4a^2-a^2\)
\(\Leftrightarrow AC=\sqrt{3a^2}=a\sqrt{3}\)
a) Tỉ số lượng giác của góc B là:
\(\sin B=\frac{a\sqrt{3}}{2a}=\frac{\sqrt{3}}{2}\)
\(\cos B=\frac{a}{2a}=\frac{1}{2}\)
\(\tan B=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\cot B=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}\)
b) Tỉ số lượng giác của góc C là:
\(\sin C=\cos B=\frac{1}{2}\)( Định lí )
\(\cos C=\sin B=\frac{\sqrt{3}}{2}\)( Định lí )
\(\tan C=\cot B=\frac{1}{\sqrt{3}}\)( Định lí )
\(\cot C=\tan B=\sqrt{3}\)( Định lí )
Chúc bn hok tốt
CM
17 tháng 1 2019
Sử dụng các tỉ số lượng giác, tính được:
sinB = 3 5 ; cosB = 4 5 ; tanB = 3 4 ; cotB = 4 3
=> sinA = 4 5 ; cosA = 3 5 ; tanA = 4 3 ; cotA = 3 4
H9
HT.Phong (9A5)
CTVHS
24 tháng 9 2023
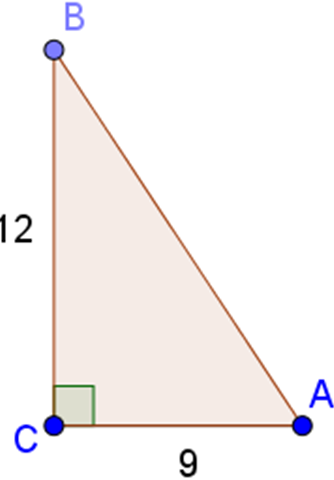
Xét ΔABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{AB^2+\left(2AB\right)^2}=AB\sqrt{5}\)
Mà:
\(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}=\dfrac{AB}{AB\sqrt{5}}=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\\cosC=\dfrac{AC}{BC}=\dfrac{2AB}{AB\sqrt{5}}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\\tanC=\dfrac{AB}{AC}=\dfrac{AB}{2AB}=\dfrac{1}{2}\\cotC=\dfrac{AC}{AB}=\dfrac{2AB}{AB}=2\end{matrix}\right.\)
24 tháng 7 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=AB^2+BC^2\)
\(\Leftrightarrow AC^2=3^2+4^2=25\)
hay AC=5(cm)
Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{AC}=\dfrac{4}{5};\cos\widehat{A}=\dfrac{AB}{AC}=\dfrac{3}{5};\)
\(\tan\widehat{A}=\dfrac{BC}{BA}=\dfrac{4}{3};\cot\widehat{C}=\dfrac{BA}{BC}=\dfrac{3}{4}\)
QT
23 tháng 9 2022
Áp dụng ĐLPTG, ta có:
AC²=AB²+BC²
<=>AC²=3²+4²=25
<=>AC=5(cm)
Xét tam giác ABC vuông tại B ta có:
Sin A=4/5 cos A=3/5 tg A=3/4 cost A=4/3
30 tháng 6 2021
Áp dụng định lí pytago vào Δvuông ABC có:
AB²=AC²+BC²=0,9²+1,2²=2,25
⇒AB=1,5(cm)
Có góc A và góc B phụ nhau, ta có:
sin B = cosA= AC/AB = 3/5
cos B = sin A = BC/AB = 4/5
tan B = cot A = AC/BC = 3/4
cot B = tan A = BC/AC = 4/3
30 tháng 6 2021
Ta có: AC = 0,9m = 9dm; BC = 1,2m = 12dm
Theo định lí Pitago, ta có:
Vì ∠A và ∠B là hai góc phụ nhau nên suy ra:
Bạn tham khảo nha
28 tháng 9 2021
cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C
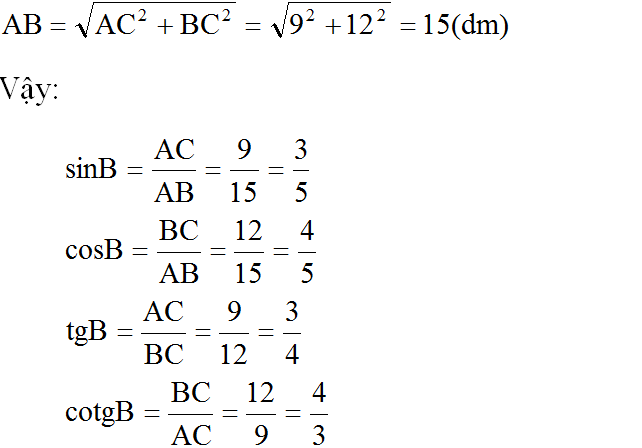
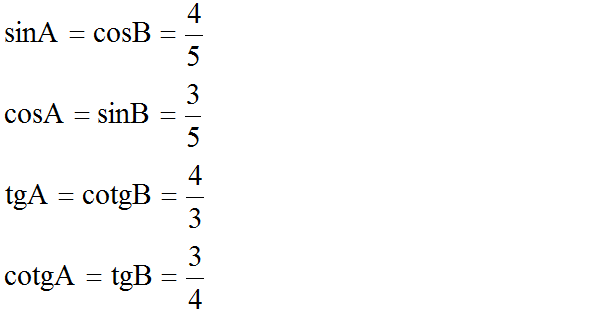
trong tam giác ABC vuông tại A có\(sinC=\frac{AB}{BC}=\frac{1}{2}\)
ta có \(sin^2C+cos^2C=1\Rightarrow cos^2C=1-\frac{1}{4}=\frac{3}{4}\) \(\Rightarrow cosC=\frac{\sqrt{3}}{2}\)
lại có \(\frac{sinC}{cosC}=tanC\Rightarrow tanC=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\)
lại có \(tanC\cdot cotgC=1\Rightarrow cotgC=\frac{1}{\frac{1}{\sqrt{3}}}=\sqrt{3}\)