Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

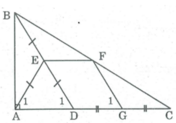
* Trong ∆ BDC, ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
Suy ra EF là đường trung bình của tam giác BCD
⇒ EF // DC hay EF // AG
Suy ra tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
Nên FG là đường trung bình của tam giác BCD
⇒ FG // BD ⇒ ∠ G 1 = ∠ D 1 (đồng vị) (1)
* Trong tam giác ABD vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BD
⇒ AE = ED = 1/2 BD (tính chất tam giác vuông)
Suy ra: tam giác AED cân tại E nên ∠ A 1 = ∠ D 1 (2)
Từ (1) và (2) suy ra: ∠ A 1 = ∠ G 1
Vậy hình thang AEFG là hình thang cân.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

a, Xét △ABC vuông tại A và △MDC vuông tại M
Có: ∠ACB là góc chung
=> △ABC ᔕ △MDC (g.g)
b, Xét △ABC vuông tại A có: AB2 + AC2 = BC2 (định lý Pytago)
=> 362 + 482 = BC2 => BC2 = 3600 => BC = 60 (cm)
Vì M là trung điểm BC (gt) => MB = MC = BC : 2 = 60 : 2 = 30 (cm)
Vì △ABC ᔕ △MDC (cmt) \(\Rightarrow\frac{AB}{MD}=\frac{AC}{MC}\) \(\Rightarrow\frac{36}{MD}=\frac{48}{30}\)\(\Rightarrow MD=\frac{36.30}{48}=22,5\) (cm)
và \(\frac{AC}{MC}=\frac{BC}{DC}\)\(\Rightarrow\frac{48}{30}=\frac{60}{DC}\)\(\Rightarrow DC=\frac{30.60}{48}=37,5\) (cm)
c, Xét △BME vuông tại M và △BAC vuông tại A
Có: ∠MBE là góc chung
=> △BME ᔕ △BAC (g.g)
\(\Rightarrow\frac{BM}{AB}=\frac{BE}{BC}\) \(\Rightarrow\frac{30}{36}=\frac{BE}{60}\)\(\Rightarrow BE=\frac{30.60}{36}=50\) (cm)
Vì M là trung điểm BC (gt) mà ME ⊥ BC (gt)
=> ME là đường trung trực BC
=> EC = BE
Mà BE = 50 (cm)
=> EC = 50 (cm)
e, Ta có: \(\frac{S_{\text{△}MDC}}{S_{\text{△}ABC}}=\frac{\frac{1}{2}.MD.MC}{\frac{1}{2}.AB.AC}=\frac{22,5.30}{36.48}=\frac{675}{1728}=\frac{25}{64}\)
P/s: Sao nhiều câu cùng tính EC vậy? Pls, không làm loãng câu hỏi
Bài làm
@Mấy bạn bên dưới: nghiêm cấm không trả lời linh tinh, nhất bạn luffy toán học, bạn rảnh đến nỗi cũng hùa theo họ mà spam linh tinh à.
a) Xét tam giác ABC và tam giác MDC có:
\(\widehat{BAC}=\widehat{DMC}=90^0\)
\(\widehat{BCA}\)chung
=> Tam giác ABC ~ tam giác MDC ( g - g )
b) Xét tam giác ABC vuông tại A có:
Theo pytago có:
BC2 = AB2 + AC2
hay BC2 = 362 + 482
hay BC2 = 1296 + 2304
=> BC2 = 3600
=> BC = 60 ( cm )
Mà M là trung điểm BC
=> BM = MC = BC/2 = 60/2 = 30 ( cm )
Vì tam giác ABC ~ tam giác MDC ( cmt )
=> \(\frac{AB}{MD}=\frac{BC}{DC}=\frac{AC}{MC}\)
hay \(\frac{36}{MD}=\frac{60}{DC}=\frac{48}{30}\)
=> \(MD=\frac{36.30}{48}=22,5\left(cm\right)\)
=> \(DC=\frac{60.30}{48}=37,5\left(cm\right)\)
c) Xét tam giác MBE và tam giác ABC có:
\(\widehat{BME}=\widehat{BAC}=90^0\)
\(\widehat{ABC}\)chung
=> Tam giác MBE ~ tam giác ABC ( g - g )
=> \(\frac{ME}{AC}=\frac{BM}{AB}\)
hay \(\frac{ME}{48}=\frac{30}{36}\Rightarrow ME=\frac{48.30}{36}=40\left(cm\right)\)
Xét tam giác MEC vuông tại M có:
EC2 = MC2 + ME2
hay EC2 = 302 + 402
=> EC2 = 900 + 1600
=> EC2 = 50 ( cm )
a) Vì tam giác MDC ~ Tam giác ABC
=> \(\frac{S_{\Delta MDC}}{S_{\Delta ABC}}=\left(\frac{MD}{AB}\right)^2=\left(\frac{22,5}{36}\right)^2=\left(\frac{5}{8}\right)^2=\frac{25}{36}\)
Câu c, d và câu đ giống nhau ?