Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\widehat{B}+\widehat{C}=90^o\)
\(\Rightarrow\cos C=\sin B=\frac{1}{3}\)
Ta có : \(\sin^2C+\cos^2C=1\Rightarrow\sin^2C=1-\cos^2C=\frac{8}{9}\)
\(\Rightarrow\sin C=\frac{2\sqrt{2}}{9}\)

Ta có: \(\dfrac{HC}{AC}=\dfrac{1}{3}\)
nên AC=3HC
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AH^2+HC^2=AC^2\)
\(\Leftrightarrow9HC^2-HC^2=4^2=16\)
\(\Leftrightarrow HC=\sqrt{2}\left(cm\right)\)
\(\Leftrightarrow AC=3\cdot HC=3\sqrt{2}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H,ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=4^2+2^2=20\)
hay \(AB=2\sqrt{5}\left(cm\right)\)

cotC=1/tanC = 4/3
=>\(\frac{ac}{ab}=\frac{4}{3}\)=>ac=4k , ab=3k {với k \(\ge\) 0 }
=>BC = 5k
=>sinC =\(\frac{3}{5}\)
cosC=\(\frac{4}{5}\)
tick nha

\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)
\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)
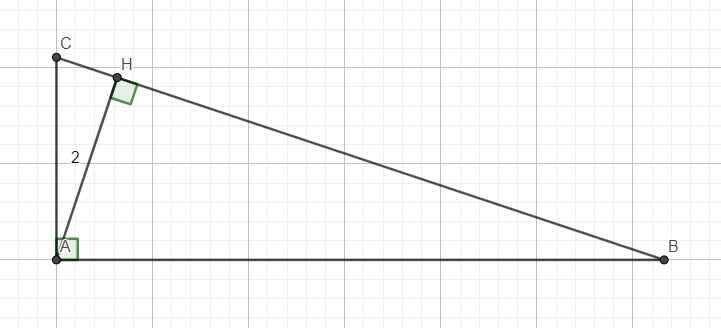
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình

Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)