Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC vuông tại B
nên \(\widehat{A}+\widehat{C}=90^0\)
hay \(\widehat{C}=23^0\)
Xét ΔABC vuông tại B có
\(AC=\dfrac{AB}{\cos67^0}\)
\(\Leftrightarrow AC\simeq20,47\left(cm\right)\)
\(\Leftrightarrow BC\simeq18,84\left(cm\right)\)

a:
ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>\(BC^2=25+64=89\)
=>\(BC=\sqrt{89}\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}=\dfrac{8}{5}\)
=>\(\widehat{B}\simeq58^0\)
=>\(\widehat{C}=32^0\)
b: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
ΔAHB vuông tại H có HM vuông góc AB
nên AM*AB=AH^2; BM*BA=BH^2; AM*MB=HM^2
ΔAHC vuông tại H có HN làđường cao
nên AN*AC=AH^2;CN*CA=CH^2; NA*NC=NH^2
AM*MB+NA*NC
=HM^2+HN^2
=MN^2
c: AB^2/AC^2
\(=\dfrac{BH\cdot CB}{CH\cdot CB}=\dfrac{BH}{CH}\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)

Lời giải:
Ta có:
$\sin B = \frac{AC}{BC}\Rightarrow AC=BC.\sin B$
$\Rightarrow AC=8\sin 50^0=6,1$ (cm)

Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos30^0=4\sqrt{3}\simeq6,928\left(cm\right)\)
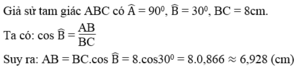
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan25^0\)
\(\Leftrightarrow AC=8\cdot\tan25^0\)
hay \(AC\simeq3,730\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+3.73^2=77,9129\)
hay \(BC\simeq8,827\left(cm\right)\)