Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)
e) Nếu AEBM là hình vuông
thì Â= Ê= góc B= góc M= 90 độ
=>AM vuông góc BC
=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông

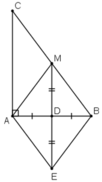
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

https://coccoc.com/search?query=cho+tam+gi%C3%A1c+abc+vu%C3%B4ng+t%E1%BA%A1i+a+am+l%C3%A0+trung+tuy%E1%BA%BFn
Theo link nàyyy

a, ta có E là điểm đối xứng với M qua D
=> me vuông góc vs md(t/c đối xứng)
xét tứ giác admn có
góc dan=90 độ
góc anm =90 độ
góc adm = 90 độ (d thuộc me)
=>tứ giác admn laf hcn
b,ta có d là trung điểm của ab
=>da=db(1)
lại có E là điểm đối xứng với M qua D
=> md=de(2)
từ 1 và 2 => từ giác aebm là hbh(3)
mà từ cma có me vuông góc vs md(t/c đối xứng)(4)
từ 3 và 4
=> từ giác aebm là hthoi
c, từ cmb có aebm là hthoi
=> ae=bm(t/c hthoi)
mà bm = cm =>ae=cm(1)
lại có da vuông góc cs me (t/c đối xứng), da vuông góc vs ac ( ab vuông góc vs ac, d thuộc ab)
=>me // ac (2)
từ 1 và 2 => tứ giác AEMC là hình bình hành
tcks cho nhé