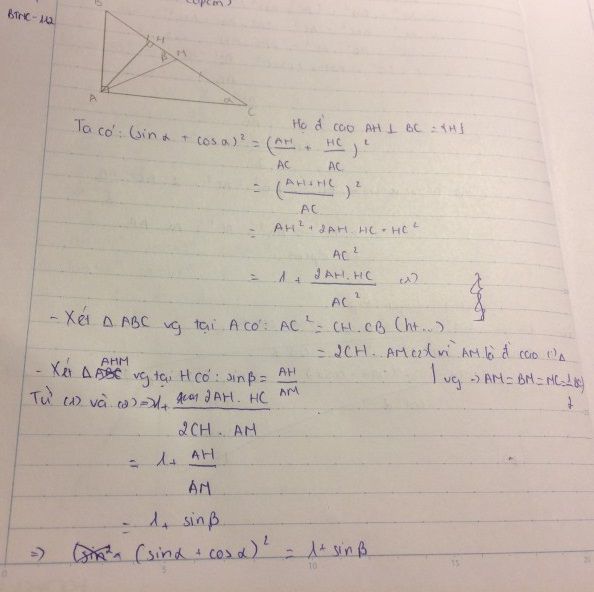Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M H
Ta có : \(\left(sin\alpha+cos\alpha\right)^2=sin^2\alpha+cos^2\alpha+2sin\alpha.cos\alpha\) (1)
Lại có : \(sin^2\alpha=\frac{AB^2}{BC^2}\) ; \(cos^2\alpha=\frac{AC^2}{BC^2}\) \(\Rightarrow sin^2\alpha+cos^2\alpha=\frac{AB^2+AC^2}{BC^2}=\frac{BC^2}{BC^2}=1\) (2)
Kẻ đường cao AH (H thuộc BC)
Ta sẽ chứng minh \(sin\beta=2sin\alpha.cos\alpha\)
Xét tam giác vuông HMA có : \(sin\beta=\frac{AH}{AM}\)
Lại có \(AH=\frac{AB.AC}{BC}\) ; \(AM=\frac{BC}{2}\) \(\Rightarrow sin\beta=\frac{\frac{AB.AC}{BC}}{\frac{BC}{2}}=\frac{2AB.AC}{BC^2}=2.\frac{AB}{BC}.\frac{AC}{BC}=2sin\alpha.cos\alpha\)(3)
Từ (1) , (2) , (3) ta có điều phải chứng minh.

A B C M H
Kẻ đường cao AH ; Vì AB < AC => BH < HC=> H thuộc BM
Ta có: \(\sin\alpha=\frac{AB}{BC};\cos\alpha=\frac{AC}{BC};\sin\beta=\frac{AH}{AM}\)
=> \(\left(\sin\alpha+\cos\alpha\right)^2=\left(\frac{AB}{BC}+\frac{AC}{BC}\right)^2=\frac{AB^2}{BC^2}+\frac{AC^2}{BC^2}+\frac{2AB.AC}{BC^2}=1+\frac{2AB.AC}{BC^2}\)
Mà theo hệ thức lượng: \(AB^2=BC.BH;AC^2=CB.CH\)
=> \(\frac{2AB.AC}{BC^2}=2.\frac{AB}{BC}.\frac{AC}{BC}=\frac{2BH.CH}{AB.AC}=\frac{2AH^2}{AB.AC}\)
Ta cần chứng minh: \(\frac{2AH^2}{AB.AC}=\frac{AH}{AM}\Leftrightarrow2AH.AM=AB.AC\Leftrightarrow AH.BC=AB.AC\)đúng
Vậy \(1+\frac{2AB.AC}{BC^2}=1+\frac{AH}{AM}\)
=> Có điều cần phải cm

Ta co:
Vì tam ABC vuông tại A co D là trung điểm BC nên \(\widehat{MAC}=\widehat{MCA}=\frac{\widehat{AMB}}{2}\)
\(\Rightarrow\beta=2\alpha\)
Từ đây ta co:
\(cos^2\alpha-sin^2\alpha=cos\left(2\alpha\right)=cos\beta\)

Ah chăc câu này ghi nhầm đề nên ghi lại câu kia đung không. Thôi xem câu trên đi