Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

"First" , ZzZ_Tiểu Thư Họ Vương_ZzZ dễ thì giải, tôi cũng đang thắc mắc
"second", đường tròn tâm O bán kính BC hay đường kính BC ?
"third ", đã vẽ hình trực quan, và tam giác EBF ko cân, sao đây......

a/ A và H cùng nhìn BC dưới 1 góc vuông => A và H nằm trên cùng 1 đường tròn đường kính BC
=> Tứ giác AHBC là tứ giác nội tiếp
b/ Xét tam giác vuông ABE và tam giác vuông HCE có
BE vuông góc với CH
AB vuông góc với CE
=> ^ABE=^HCE (góc có cạnh tương ứng vuông góc)
=> tam giác ABE đồng dạng với tam giác HCE
=> \(\frac{EA}{EH}=\frac{EB}{EC}\Rightarrow EA.EC=EH.EB\)
c/ Xét tam giác EBC có
BA vuông góc CE
CH vuông góc với BE
=> D là trực tâm của tam giác EBC => ED là đường cao của tam giác EBC => ED vuông góc với BC
Ta có:
ED vuông góc với BC
CE vuông góc với AB
=> ^CED = ^ABC (góc có cạnh tương ứng vuông góc)
^ABC=^ACB=(180 - ^BAC)/2 = 45
=> ^CED=45
Xét tam giác vuông ADE có ^ADE=(180 - CED - DAE) = (180 - 45 - 90) = 45
=> ^CED = ^ADE
=> Tam giác ADE cân tại A => AD=AE

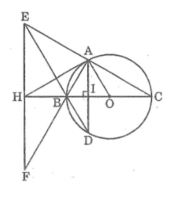
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.

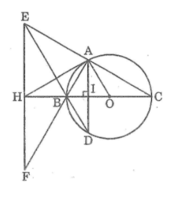
Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
Do \(CA=CB=a\) nên \(BE.BC+AC.AK=a\left(AK+BE\right)\)
Ta chứng minh \(AK+BE\) không đổi. Thật vậy, gọi P là giao điểm của KE và AB. Quan sát thấy E là trực tâm tam giác ABK \(\Rightarrow KP\perp AP\) tại P. Lại có \(\widehat{KAP}=45^o\) nên suy ra \(\widehat{AKP}=45^o\). Từ đó suy ta tam giác CEK cân tại C hay \(CE=CK\).
Từ đó \(AK+BE=AC+CK+BC-CE=2a\). Vậy \(BE.BC+AC.AK=2a^2\) không đổi (đpcm)