Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

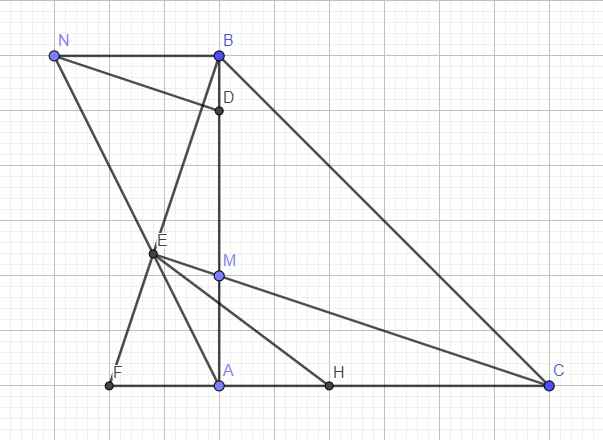
Góc α: Góc giữa C, A, B Góc α: Góc giữa C, A, B Góc β: Góc giữa N, B, A Góc β: Góc giữa N, B, A Đoạn thẳng f: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, C] Đoạn thẳng i: Đoạn thẳng [B, A] Đoạn thẳng l: Đoạn thẳng [B, N] Đoạn thẳng m: Đoạn thẳng [N, A] Đoạn thẳng r: Đoạn thẳng [B, F] Đoạn thẳng s: Đoạn thẳng [F, A] Đoạn thẳng t: Đoạn thẳng [E, C] Đoạn thẳng a: Đoạn thẳng [N, J] Đoạn thẳng b: Đoạn thẳng [E, H] A = (0.92, -1.12) A = (0.92, -1.12) A = (0.92, -1.12) A = (0.92, -1.12) A = (0.92, -1.12) A = (0.92, -1.12) A = (0.92, -1.12) C = (6.4, -1.14) C = (6.4, -1.14) C = (6.4, -1.14) C = (6.4, -1.14) C = (6.4, -1.14) C = (6.4, -1.14) C = (6.4, -1.14) Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm M: Giao điểm đường của d, i Điểm F_1: Trung điểm của B, M Điểm F_1: Trung điểm của B, M Điểm E_1: Trung điểm của B, A Điểm E_1: Trung điểm của B, A Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm N: Giao điểm đường của e, k Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm E: Giao điểm đường của n, m Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm F: Giao điểm đường của p, q Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm J: Trung điểm của B, F_1 Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C Điểm H: Trung điểm của F, C
a) Gọi J là điểm thuộc AB sao cho BJ = AB/6
Ta có AM = AB/3 nên AM = 2BJ
Lại có BN = AB/2 mà AB = AC nên AC = 2BN
Vậy thì ta có ngay \(\Delta NBJ\sim\Delta CAM\left(c-g-c\right)\)
\(\Rightarrow\widehat{BNJ}=\widehat{ACM}\)
Lại có NB // AC nên NJ // EM
Xét tam giác ANJ có NJ // EM, áp dụng đinh lý Pitago ta có:
\(\frac{EA}{NE}=\frac{MA}{MJ}=\frac{2}{3}\)
Mà BN // FC (Cùng vuông góc AB) nên áp dụng định lý Ta let ta cũng có:
\(\frac{AF}{BN}=\frac{EA}{NE}=\frac{2}{3}\)
Mà \(\frac{AM}{BN}=\frac{2}{3}\Rightarrow AM=AF\)
b) Đặt BJ = a
Khi đó ta có \(AF=AM=2a;AC=6a;\)
\(NJ=\sqrt{9a^2+a^2}=a\sqrt{10}\Rightarrow EM=\frac{2a\sqrt{10}}{5}\)
\(BF=\sqrt{4a^2+36a^2}=2a\sqrt{10}\Rightarrow EF=\frac{4a\sqrt{10}}{3}\)
Ta thấy rằng \(EF^2+EC^2=64a^2=FC^2\) nên tam giác EFC vuông tại E.
Theo tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có :
FH = EH = HC
Vậy nên EH = FH = FC/2 = 8a/2 = 4a = BM.

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

Qua N kẻ đường thẳng song song CM cắt AB tại D
\(\Rightarrow\widehat{BND}=\widehat{ACM}\) (góc có cạnh tương ứng song song)
\(\Rightarrow\Delta_VBND\sim\Delta_VACM\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{BN}=\dfrac{AM}{AC}=\dfrac{1}{3}\Rightarrow BD=\dfrac{1}{3}BN=\dfrac{1}{6}AB\)
\(\Rightarrow MD=AB-AM-BD=AB-\dfrac{1}{3}AB-\dfrac{1}{6}AB=\dfrac{1}{2}AB\)
Áp dụng Talet: \(\dfrac{AF}{BN}=\dfrac{AE}{NE}=\dfrac{AM}{MD}=\dfrac{\dfrac{1}{3}AB}{\dfrac{1}{2}AB}=\dfrac{2}{3}\)
\(\Rightarrow AF=\dfrac{2}{3}BN=\dfrac{2}{3}.\dfrac{1}{2}AB=\dfrac{1}{3}AB=AM\left(đpcm\right)\)
b.
Ta có: \(CF=AF+AC=\dfrac{1}{3}AB+AB=\dfrac{4}{3}AB\)
\(BF=\sqrt{AB^2+AF^2}=\sqrt{AB^2+\left(\dfrac{1}{3}AB\right)^2}=\dfrac{AB\sqrt{10}}{3}\)
\(\dfrac{EM}{ND}=\dfrac{AM}{AD}=\dfrac{\dfrac{1}{3}AB}{\dfrac{5}{6}AB}=\dfrac{2}{5}\Rightarrow EM=\dfrac{2}{5}ND=\dfrac{AB\sqrt{10}}{15}\)
\(\dfrac{BE}{EF}=\dfrac{BN}{AF}=\dfrac{\dfrac{1}{2}AB}{\dfrac{1}{3}AB}=\dfrac{3}{2}\Rightarrow\dfrac{BE}{BF-BE}=\dfrac{3}{2}\)
\(\Rightarrow BE=\dfrac{3}{5}BF=\dfrac{AB\sqrt{10}}{5}\)
\(\Rightarrow BE^2+EM^2=\dfrac{2}{5}AB^2+\dfrac{2}{45}AB^2=\dfrac{4}{9}AB^2=\left(\dfrac{2}{3}AB\right)^2=BM^2\)
\(\Rightarrow\Delta BEM\) vuông tại E \(\Rightarrow\Delta CEF\) vuông tại E
\(\Rightarrow EH\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow EH=\dfrac{1}{2}CF=\dfrac{2}{3}AB=BM\)

Cho t/giác ABC cân tại A. Trên cạnh AB lấy điểm E. Trên tia đối của tia CA lấy điểm F sao cho CF=BE. Vẽ tia Bx vuông góc AB & Cy vuông góc AC. Gọi I là giao điểm của Bx và Cy
a, C/m t/giác IEF cân
b, Vẽ qua E đường thẳng song song với BC cắt AC tại D. C/m CD=CF
c, Gọi H là Giao điểm của EF và BC. C/m E, F đối xứng qua IH
Câu a ,b mình biết làm rồi còn câu c nữa thôi. SIN LOI MINH KO BIET LAM

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.