Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ \(BN\perp AH\left(N\in AC\right)\)
Khi đó \(BN//IK\)(cùng vuông góc với AH)
Kết hợp với I là trung điểm của BM suy ra IK là đường trung bình của \(\Delta MBC\)
\(\Rightarrow\)K là trung điểm của MN
hay MK = NK kết hợp giả thiết AK = CK suy ra AN = CM (cộng theo vế) (1)
Xét \(\Delta ABN\)và \(\Delta CAH\)có:
AB = CA (gt)
\(\widehat{ABN}=\widehat{CAH}\)(cùng phụ với \(\widehat{BAH}\))
Do đó \(\Delta ABN=\Delta CAH\left(cgv-gnk\right)\)
\(\Rightarrow AN=CH\)(hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra CH = CM
Mà \(\widehat{HCM}=90^0\)suy ra \(\Delta HCM\)vuông cân tại C
Vậy \(\widehat{HMC}=45^0\)

đề sai rồi
QUA C KẺ ĐƯỜNG VUÔNG GÓC VỚI AC, CHÚNG CẮT NHAU TẠI H
2 ĐIỂM C VÀ H TRÙNG NHAU thì sao lại có
CMR TAM GIÁC MHC VUÔNG CÂN

a/Ta có H, K lận lượt là hình chiếu của B và C trên tia Ax (gt)
Gọi N là giao điềm của Ax với BC
Khi đó ta có:
+Tam giác BHN vuông tại H => BH=<BN(1)
+Tam giác CKN vuông tại K => CK=<CN (2)
Cộng 2 vế của (1) và (2) ta được:
BH+CK=<BN+CN hay BH+CK=<BC (đpcm) (3)
b/ Từ (3) => Tổng BH+CK lớn nhất khi BH+CK=BC
<=> H trùng N và K trùng N
<=> AN vuông góc với BC tại N
<=> Ax là tia chứa đường cao xuất phát từ đỉnh A của tam giác ABC
olm duyệt

a: \(\widehat{HMC}=30^0\)
b: Xét ΔMHC vuông tại H và ΔMKA vuông tại K có
MC=MA
\(\widehat{CMH}=\widehat{AMK}\)
Do đó: ΔMHC=ΔMKA
Suy ra: MH=MK
Xét tứ giác AHCK có
M là trung điểm của AC
M là trung điểm của HK
Do đó: AHCK là hình bình hành
Suy ra: AH//CK

a) Xét ΔBAK vuông tại A và ΔBCK vuông tại C có
BK chung
BA=BC(ΔBAC cân tại B)Do đó: ΔBAK=ΔBCK(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABK}=\widehat{CBK}\)(hai góc tương ứng)
mà tia BK nằm giữa hai tia BA,BC
nên BK là tia phân giác của \(\widehat{ABC}\)(đpcm)
b) Ta có: ΔBAK=ΔBCK(cmt)
nên KA=KC(Hai cạnh tương ứng)
Ta có: BA=BC(ΔABC cân tại B)
nên B nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có:KA=KC(cmt)
nên K nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng) (2)
Từ (1) và (2) suy ra BK là đường trung trực của AC
hay BK\(\perp\)AC(đpcm)
Vì BK là đường trung trực của AC(cmt)
nên BK vuông góc với AC tại trung điểm của AC
mà BK cắt AC tại I(gt)
nên BK\(\perp\)AC tại I và I là trung điểm của AC
Ta có: I là trung điểm của AC(cmt)
nên \(CI=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBIC vuông tại I, ta được:
\(BC^2=BI^2+IC^2\)
\(\Leftrightarrow BI^2=BC^2-IC^2=10^2-3^2=91\)
hay \(BI=\sqrt{91}cm\)
Vậy: \(BI=\sqrt{91}cm\)
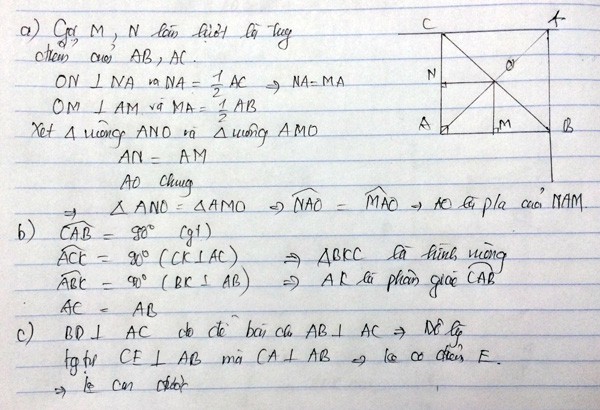
Hhh bài nay mk chịu òi, xl bn nha!!!mk lp 7 mà k giỏi về Toán ( hình hk) , Hhh!